تعامد

تعامد (جبر خطی). در ریاضیات، دو بردار را متعامد[ ۱] ( به انگلیسی: Orthogonal ) گویند هرگاه برهم قائم باشند. به عبارت دیگر دو بردار متعامدند اگر و تنها اگر ضرب داخلی آنها برابر با صفر باشد یا با هم زاویهٔ راست ( ۹۰ درجه ) ساخته باشند.
• در هندسه، دو بردار اقلیدسی عمود بر هم هستند اگر به بکدیگر قائم باشن؛ یعنی هم زاویه قائم بسازند.
• دو بردار x {\displaystyle x} و y {\displaystyle y} را در یک فضای ضرب داخلی V {\displaystyle V} برهم عمودند اگر ضرب داخلی ⟨ x , y ⟩ {\displaystyle \langle x, y\rangle } صفر باشد. این رابطه تعامد را با x ⊥ y {\displaystyle x\perp y} نشان می دهند.
• دو زیرفضای برداری A {\displaystyle A} و B {\displaystyle B} از یک فضای ضرب داخلی V {\displaystyle V} را زیرفضاهای متعامد می گوییم اگر هر بردار از A {\displaystyle A} به هر بردار از B {\displaystyle B} عمود باشد. بزرگ ترین زیرفضایی که به یک زیرفضا عمود باشد، متمم عمود آن نامیده می شود.
• یک نگاشت خطی T : V → V {\displaystyle T:V\rightarrow V} را نگاشت خطی متعامد می گوییم اگر ضرب داخلی را پایسته نگه دارد. یعنی برای هر جفت بردار x {\displaystyle x} و y {\displaystyle y} در فضای ضرب داخلی V {\displaystyle V} داشته باشیم:
این یعنی T زاویهٔ بین x و y را ثابت نگه می دارد و طول T x و x برابر است.
دسته ای از بردارهای دوبه دو عمود برهم را که طول واحد داشته باشند ( بردار یکّه باشند ) بردارهای یکّه راست هنجار ( متعامد یکه ) می نامیم.
مرسوم است که برای توابع f و g ضرب داخلی زیر را تعریف کنیم:
⟨ f , g ⟩ w = ∫ a b f ( x ) g ( x ) w ( x ) d x .
که در آن w ( x ) تابع وزن نامنفی برای ضرب داخلی است. در ساده ترین حالت w ( x ) = 1. در این صورت، اگر حاصل ضرب داخلی شان صفر باشد می گوییم دو تابع برهم عمودند:
∫ a b f ( x ) g ( x ) w ( x ) d x = 0.
با استفاده از ضرب داخلی، ما نُرم به صورت زیر تعریف میکنیم که عبارت است از ضرب داخلی بردار در خودش. نُرم، طول بردارها ( تابع ها ) را به دست می د:
‖ f ‖ w = ⟨ f , f ⟩ w
اعضای یک دنباله از توابع {fi  : i = 1, 2, 3, . . . } متعامد هستند اگر
⟨ f i , f j ⟩ = ∫ − ∞ ∞ f i ( x ) f j ( x ) w ( x ) d x = ‖ f i ‖ 2 δ i , j = ‖ f j ‖ 2 δ i , j

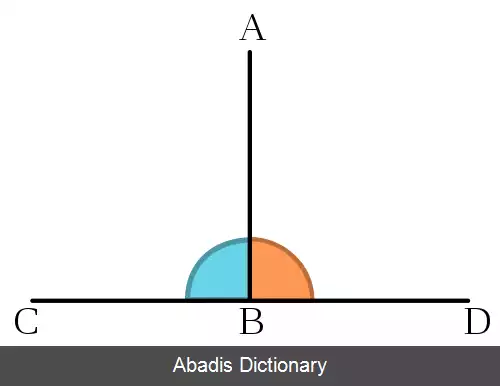
تعامد (هندسه). در هندسهٔ مقدماتی، واژهٔ عمود رابطهٔ دو خط را توصیف می کند که با زاویهٔ قائمه با یکدیگر تقاطع می کنند. یعنی زمانی گفته می شود یک خط بر یک خط دیگر عمود است که آن دو خط با یکدیگر زاویهٔ قائمه بسازند. [ ۱]
تعامد، یک رابطهٔ متقارن است، یعنی زمانی که خط ۱ بر خط ۲ عمود باشد، خط ۲ هم بر خط ۱ عمود است. بنابراین، معمولاً تنها گفته می شود که دو خط برهم عمودند و ترتیبی ذکر نمی شود.