مش ساده ترین حلقه ای است که شاخه ای درون آن نباشد؛ از همین رو مش، فقط در مدارهای مسطح ( یعنی مدارهایی که روی کاغذ بتوان رسم کرد بدون اینکه شاخه ها یکدیگر را قطع کنند مگر در گره ها ) تعریف می شود.
• تبدیل منابع جریان به ولتاژ، در صورت امکان.
• شماره گذاری مش ها؛ و تعیین جهت ساعت گرد برای جریان آنها[ نیازمند منبع]
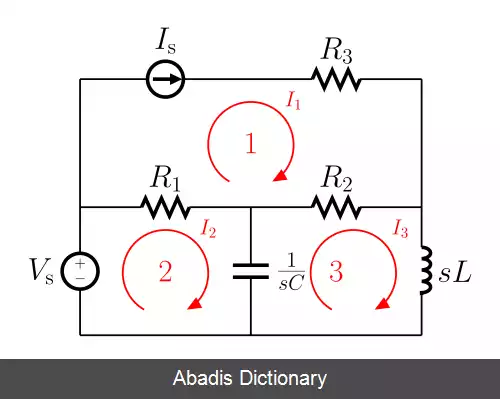
• جریان شاخهٔ هر مش هم جهت همان مش و هم اندازهٔ آن است و برای شاخه های مشترک بین دو مش برابر تفاضل آنهاست.
• نوشتن KVL ( قانون ولتاژ کیرشهف ) در تمام مش ها و برحسب جریان مش ها. در صورتی که یک منبع جریان مستقل یا وابسته بین دو مش وجود داشته باشد در این دو مش نمی توان قانون ولتاژ کیرشهف را نوشت زیرا ولتاژ منبع جریان نامعلوم است. در نتیجه دو معادله از دست می رود. راه حل این است که یک مش مرکب که از دو مش مذکور تشکیل شده در نظر بگیریم و قانون ولتاژ کیرشهف را برای آن مش مرکب بنویسیم. به این ترتیب یکی از دو معادله از دست رفته به دست می آید. معادله دیگر نیز با استفاده از رابطه منبع جریان بدست می آید. [ ۱]
• به این ترتیب یک دستگاه معادله خطی بدست می آید که به راحتی قابل حل است.
{ Mesh 1: I 1 = I s Mesh 2: − V s + R 1 ( I 2 − I 1 ) + 1 s c ( I 2 − I 3 ) = 0 Mesh 3: 1 s c ( I 3 − I 2 ) + R 2 ( I 3 − I 1 ) + L s I 3 = 0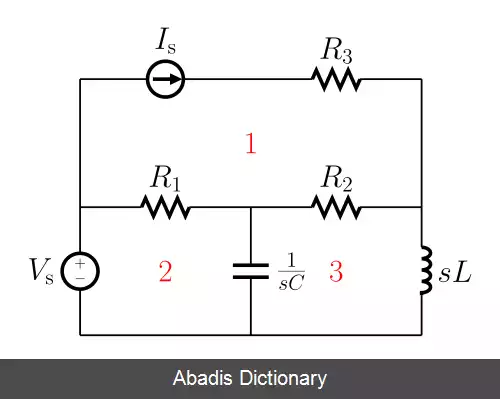
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف• تبدیل منابع جریان به ولتاژ، در صورت امکان.
• شماره گذاری مش ها؛ و تعیین جهت ساعت گرد برای جریان آنها[ نیازمند منبع]
• جریان شاخهٔ هر مش هم جهت همان مش و هم اندازهٔ آن است و برای شاخه های مشترک بین دو مش برابر تفاضل آنهاست.
• نوشتن KVL ( قانون ولتاژ کیرشهف ) در تمام مش ها و برحسب جریان مش ها. در صورتی که یک منبع جریان مستقل یا وابسته بین دو مش وجود داشته باشد در این دو مش نمی توان قانون ولتاژ کیرشهف را نوشت زیرا ولتاژ منبع جریان نامعلوم است. در نتیجه دو معادله از دست می رود. راه حل این است که یک مش مرکب که از دو مش مذکور تشکیل شده در نظر بگیریم و قانون ولتاژ کیرشهف را برای آن مش مرکب بنویسیم. به این ترتیب یکی از دو معادله از دست رفته به دست می آید. معادله دیگر نیز با استفاده از رابطه منبع جریان بدست می آید. [ ۱]
• به این ترتیب یک دستگاه معادله خطی بدست می آید که به راحتی قابل حل است.
{ Mesh 1: I 1 = I s Mesh 2: − V s + R 1 ( I 2 − I 1 ) + 1 s c ( I 2 − I 3 ) = 0 Mesh 3: 1 s c ( I 3 − I 2 ) + R 2 ( I 3 − I 1 ) + L s I 3 = 0


wiki: تحلیل مش
