در ریاضیات، تبدیل فوریه ( به انگلیسی: Fourier transform، /ˈfʊrieɪ, - iər/ ) یا ( FT ) یک تبدیل ریاضیاتی است که توابعی را که بر حسب زمان یا فضا هستند، به توابعی بر حسب فرکانس زمانی یا فضایی تجزیه می کند، مانند بیان یک آکورد موسیقی بر حسب حجم ها و فرکانس های نت های تشکیل دهنده آن. اصطلاح تبدیل فوریه هم به نمایش دامنه فرکانس و هم به عملیات ریاضی مربوط به آن که نمایش دامنه فرکانس را به تابعی از مکان یا زمان مرتبط می کند گفته می شود.
تبدیل فوریه یک تابع از زمان، یک تابع مقدار مختلط از فرکانس است، که اندازه آن ( قدر مطلق ) ، فرکانس موجود در تابع اصلی را نشان می دهد، و آرگومان آن اختلاف فاز سینوسی پایه در آن فرکانس است. تبدیل فوریه فقط محدود به توابع زمان نیست، اما به دامنه عملکرد اصلی، معمولاً دامنه زمان گفته می شود. معکوس تبدیل فوریه نیز وجود دارد که به صورت ریاضی تابع اصلی را از نمایش دامنه فرکانسی آن تولید می کند، که توسط قضیه عکس فوریه اثبات شده است.
عملیات های خطی انجام شده در یک دامنه ( زمان یا فرکانس ) در دامنه های دیگر دارای عملیات های متناظر هستند، که گاهی انجام آنها آسان تر است. عملیات مشتق گیری در دامنه زمان معادل با ضرب در فرکانس است، در نتیجه تجزیه و تحلیل برخی معادلات دیفرانسیلی در دامنه فرکانس راحت تر است. همچنین، کانولوشن در دامنه زمان معادل با ضرب معمولی در دامنه فرکانس است ( به قضیه کانولوشن مراجعه کنید ) . پس از انجام عملیات مورد نظر، می توان نتیجه را به حوزه زمان برگرداند. آنالیز هارمونیک یک مطالعه سیستماتیک از رابطه بین دامنه های فرکانس و زمان است، از جمله انواع توابع یا عملیاتی که در یکی یا دیگری «ساده تر» هستند و با بسیاری از زمینه های ریاضیات مدرن ارتباط عمیقی دارد.
تبدیل فوریه، نامیده شده به اسم ریاضیدانِ فرانسوی ژوزف فوریه، یک تبدیل انتگرالی است که هر تابع f ( t ) را به یک تابع دیگر F ( ω ) منعکس می کند. در این صورت، به F ( ω ) تبدیل فوریهٔ تابع f ( t ) می گویند. حالت خاص تبدیل فوریه، سری فوریه نام دارد و آن زمانی کاربرد دارد که تابع f ( t ) متناوب باشد، یعنی: f ( t + T ) = f ( t ) . چنانچه تابع متناوب نباشد یا به عبارتی، تناوب آن برابر بی نهایت باشد ( T → ∞ ) ، از سری فوریه عبارت زیر به دست می آید:
F ( ω ) = 1 2 π ∫ − ∞ ∞ f ( t ) e − i ω t d t


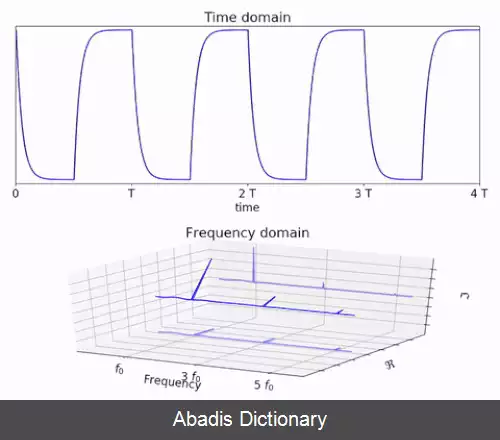
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتبدیل فوریه یک تابع از زمان، یک تابع مقدار مختلط از فرکانس است، که اندازه آن ( قدر مطلق ) ، فرکانس موجود در تابع اصلی را نشان می دهد، و آرگومان آن اختلاف فاز سینوسی پایه در آن فرکانس است. تبدیل فوریه فقط محدود به توابع زمان نیست، اما به دامنه عملکرد اصلی، معمولاً دامنه زمان گفته می شود. معکوس تبدیل فوریه نیز وجود دارد که به صورت ریاضی تابع اصلی را از نمایش دامنه فرکانسی آن تولید می کند، که توسط قضیه عکس فوریه اثبات شده است.
عملیات های خطی انجام شده در یک دامنه ( زمان یا فرکانس ) در دامنه های دیگر دارای عملیات های متناظر هستند، که گاهی انجام آنها آسان تر است. عملیات مشتق گیری در دامنه زمان معادل با ضرب در فرکانس است، در نتیجه تجزیه و تحلیل برخی معادلات دیفرانسیلی در دامنه فرکانس راحت تر است. همچنین، کانولوشن در دامنه زمان معادل با ضرب معمولی در دامنه فرکانس است ( به قضیه کانولوشن مراجعه کنید ) . پس از انجام عملیات مورد نظر، می توان نتیجه را به حوزه زمان برگرداند. آنالیز هارمونیک یک مطالعه سیستماتیک از رابطه بین دامنه های فرکانس و زمان است، از جمله انواع توابع یا عملیاتی که در یکی یا دیگری «ساده تر» هستند و با بسیاری از زمینه های ریاضیات مدرن ارتباط عمیقی دارد.
تبدیل فوریه، نامیده شده به اسم ریاضیدانِ فرانسوی ژوزف فوریه، یک تبدیل انتگرالی است که هر تابع f ( t ) را به یک تابع دیگر F ( ω ) منعکس می کند. در این صورت، به F ( ω ) تبدیل فوریهٔ تابع f ( t ) می گویند. حالت خاص تبدیل فوریه، سری فوریه نام دارد و آن زمانی کاربرد دارد که تابع f ( t ) متناوب باشد، یعنی: f ( t + T ) = f ( t ) . چنانچه تابع متناوب نباشد یا به عبارتی، تناوب آن برابر بی نهایت باشد ( T → ∞ ) ، از سری فوریه عبارت زیر به دست می آید:
F ( ω ) = 1 2 π ∫ − ∞ ∞ f ( t ) e − i ω t d t





wiki: تبدیل فوریه
