به مجموعه ای از تاس ها ناگذرا می گوییم اگر شامل سه تاس، A, B و C باشد، به صورتی که عدد تاس A به احتمال بیش از نیم، بیشتر از عدد B بوده و عدد تاس B نیز به احتمال بیش از نیم، بیشتر از C باشد، با این حال نتوان نتیجه گرفت که عدد تاس A به احتمال بیشتر از نیم از تاس C بزرگ تر است.
به عبارت دیگر، اگر رابطهٔ “ در یک آزمایش، تاس X با احتمال بیشتر از نیم عددی بزرگ تر از تاس Y دارد “ را R بنامیم، مجموعه ای از تاس ها ناگذرا است اگر رابطهٔ R بر روی زوج مرتب هایی از تاس های مجموعه دارای خاصیت تراگذری نباشد. نام این مجموعه از تاس ها نیز از همین تعریف گرفته شده است.
با استفاده از چنین مجموعه هایی از تاس ها، می توان بازی هایی اختراع کرد که نتیجهٔ آن ها به طور متوسط به نفع یکی از بازیکنان باشد.
این تاس ها در دستهٔ جامع تناقض های ناگذرا قرار می گیرند که مطالعات بسیاری حول آن انجام می گیرد. به عنوان مثال یکی از معروف ترین مسائل در ناگذرایی، پارادوکس رای گیری است که اولین بار توسط مارکی دو کندورسه مطرح شد. مسئله برای جامعه ای با سه انتخاب A و B و C است که افراد در این جامعه A را به B, B را به C و C را به A ترجیح می دهند. [ ۱]
ثابت شده است که اگر احتمال برد تاس A از B را با p، احتمال برد B از C را با q و احتمال برد C از A را با r نمایش دهیم خواهیم داشت: 1 ≤ p + q + r ≤ 2 و برای q, p و r برابر در حالت بیشینه هر کدام 2 3 هستند. اما ثابت می شود که این حالت ممکن نیست. بنابراین نمی توان به طور دقیق از تاس های ناگذرا برای مدل سازی مسئله انتخابات استفاده کرد. [ ۲]
فرض کنید یک بازی با قواعد زیر تعریف شده است:
• نفر اول تاسی انتخاب می کند.
• نفر دوم از میان تاس های باقی مانده یکی را انتخاب می کند.
• اکنون هر بازیکن یک بار تاس می اندازند و تاس با برآمد بیشتر برنده اعلام می شود.
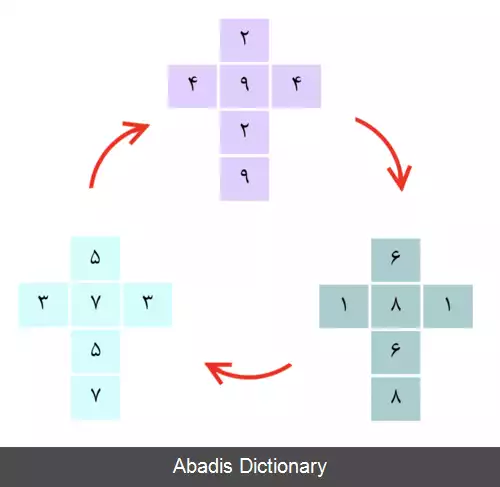
اگر این بازی با مجموعه ای از تاس های گذرا انجام شود، بازی یا عادلانه است یا به نفع اولین بازیکن، زیرا می تواند تاسی را انتخاب کند که بیشتر از نیمی از مواقع ببرد.
اما اکنون مجموعه تاس های زیر را در نظر بگیرید:
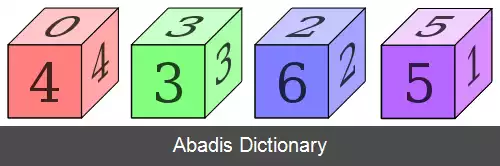
• بر روی وجه های تاس A اعداد ۲و ۲و ۴و ۴و ۹و ۹ نوشته شده اند.
• بر روی وجه های تاس B اعداد ۱و ۱و ۶و ۶و ۸و ۸ نوشته شده اند.
• بر روی وجه های تاس C اعداد ۳و ۳و ۵و ۵و ۷و ۷ نوشته شده اند.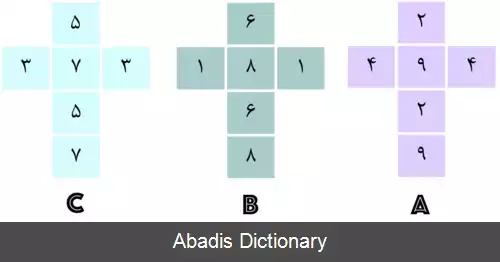
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبه عبارت دیگر، اگر رابطهٔ “ در یک آزمایش، تاس X با احتمال بیشتر از نیم عددی بزرگ تر از تاس Y دارد “ را R بنامیم، مجموعه ای از تاس ها ناگذرا است اگر رابطهٔ R بر روی زوج مرتب هایی از تاس های مجموعه دارای خاصیت تراگذری نباشد. نام این مجموعه از تاس ها نیز از همین تعریف گرفته شده است.
با استفاده از چنین مجموعه هایی از تاس ها، می توان بازی هایی اختراع کرد که نتیجهٔ آن ها به طور متوسط به نفع یکی از بازیکنان باشد.
این تاس ها در دستهٔ جامع تناقض های ناگذرا قرار می گیرند که مطالعات بسیاری حول آن انجام می گیرد. به عنوان مثال یکی از معروف ترین مسائل در ناگذرایی، پارادوکس رای گیری است که اولین بار توسط مارکی دو کندورسه مطرح شد. مسئله برای جامعه ای با سه انتخاب A و B و C است که افراد در این جامعه A را به B, B را به C و C را به A ترجیح می دهند. [ ۱]
ثابت شده است که اگر احتمال برد تاس A از B را با p، احتمال برد B از C را با q و احتمال برد C از A را با r نمایش دهیم خواهیم داشت: 1 ≤ p + q + r ≤ 2 و برای q, p و r برابر در حالت بیشینه هر کدام 2 3 هستند. اما ثابت می شود که این حالت ممکن نیست. بنابراین نمی توان به طور دقیق از تاس های ناگذرا برای مدل سازی مسئله انتخابات استفاده کرد. [ ۲]
فرض کنید یک بازی با قواعد زیر تعریف شده است:
• نفر اول تاسی انتخاب می کند.
• نفر دوم از میان تاس های باقی مانده یکی را انتخاب می کند.
• اکنون هر بازیکن یک بار تاس می اندازند و تاس با برآمد بیشتر برنده اعلام می شود.
اگر این بازی با مجموعه ای از تاس های گذرا انجام شود، بازی یا عادلانه است یا به نفع اولین بازیکن، زیرا می تواند تاسی را انتخاب کند که بیشتر از نیمی از مواقع ببرد.
اما اکنون مجموعه تاس های زیر را در نظر بگیرید:
• بر روی وجه های تاس A اعداد ۲و ۲و ۴و ۴و ۹و ۹ نوشته شده اند.
• بر روی وجه های تاس B اعداد ۱و ۱و ۶و ۶و ۸و ۸ نوشته شده اند.
• بر روی وجه های تاس C اعداد ۳و ۳و ۵و ۵و ۷و ۷ نوشته شده اند.



wiki: تاس های ناگذرا
