تابع هولومورفیک ( به انگلیسی: Holomorphic function ) در ریاضیات، یک تابع مختلط - مقدار، از یک یا بیشتر متغیر مختلط است که در همسایگی هر نقطه در دامنهاش در فضای مختصات مختلط Cn مشتق پذیر مختلط است. وجود یک مشتق مختلط در یک همسایگی، شرط بسیار قوی ای است: به معنی ضمنی آن است که یک تابع هولومورفیک بینهایت مشتق پذیر است؛ و به صورت محلی با سری تیلور خودش برابر است ( تحلیلی است ) . توابع هولومورفیک «اشیای اصلی مطالعه» در گرایش آنالیز مختلط هستند.
اگرچه اصطلاح تابع تحلیلی را اغلب بجای اصطلاح «تابع هولومورفیک» بکار می رود، واژه «تحلیلی» به صورت کلی تر تعریف شده است تا به هر تابعی ( حقیقی، مختلط، یا نوع کلی تر ) اشاره کند که آن تابع را باید بتوان بصورت یک سری توانی همگرا در همسایگی هر نقطه در دامنه اش نوشت. این موضوع که همه توابع هولومورفیک نوعی تابع تحلیلی مختلط هستند و برعکس، یک قضیه اصلی در تحلیل مختلط است. [ ۱]
به توابع هولومورفیک گاهی توابع منظم هم می گویند. [ ۲] [ ۳] به تابع هولومورفیکی که دامنه اش کل صفحه مختلط است، یک تابع تام گفته می شود. عبارت «هولومورفیک در یک نقطه z0» فقط به معنی مشتق پذیر در z0 نیست، بلکه به معنی آن است که در همه جا در همسایگی z0 در صفحه مختلط مشتق پذیر است.
اگر به ما یک تابع مختلط - مقدار از یک متغیر منفرد مختلط داده شده باشد، مشتق در یک نقطه z0 در دامنه اش توسط حد زیر تعریف می شود:[ ۴]
این مشابه تعریف مشتق برای توابع حقیقی است، فقط همه کمیت هایش مختلط هستند. بخصوص، حد موقعی گرفته می شود که عدد مختلط z به سمت z0 میل می کند، و باید برای هر دنباله مقادیر مختلط برای z که در صفحه مختلط به سمت z0 میل می کند، مقدار یکسانی داشته باشد. اگر حد موجود باشد، می گوییم که در نقطه z0 مشتق پذیر مختلط است. مفهوم مشتق پذیری مختلط ویژگی های مشترک زیادی با مشتق پذیری حقیقی دارد: خطی است و از قاعده ضرب، قاعده خارج قسمت، و قاعده زنجیره ای پیروی می کند. [ ۵]
اگر در هر نقطه z0 در یک مجموعه باز U مشتق پذیر مختلط باشد، آنوقت می گوییم که روی U هولومورفیک است. می گوییم که در نقطه z0 هرلومورفیک است اگر روی یک همسایگی z0 مشتق پذیر مختلط باشد. [ ۶] می گوییم که روی یک مجموعه غیر - باز A هولومورفیک است اگر روی یک همسایگی A هولومورفیک باشد. به عنوان یک غیر مثال، تابع f ( z ) = | z |2 دقیقا روی یک نقطه ( z0 = 0 ) مشتق پذیر مختلط نیست، و به این دلیل، در نقطه 0 هولومورفیک نیست، زیرا هیچ مجموعه بازی حول 0 موجود نیست که در آن مشتق پذیر مختلط باشد.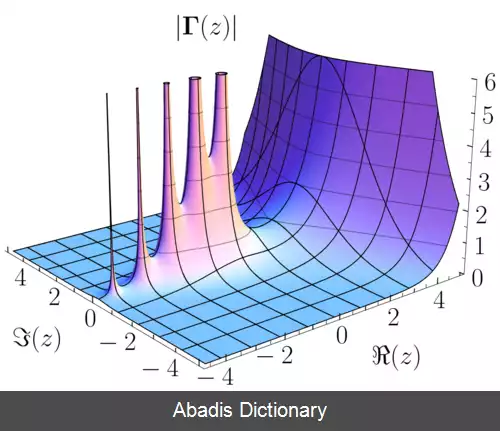
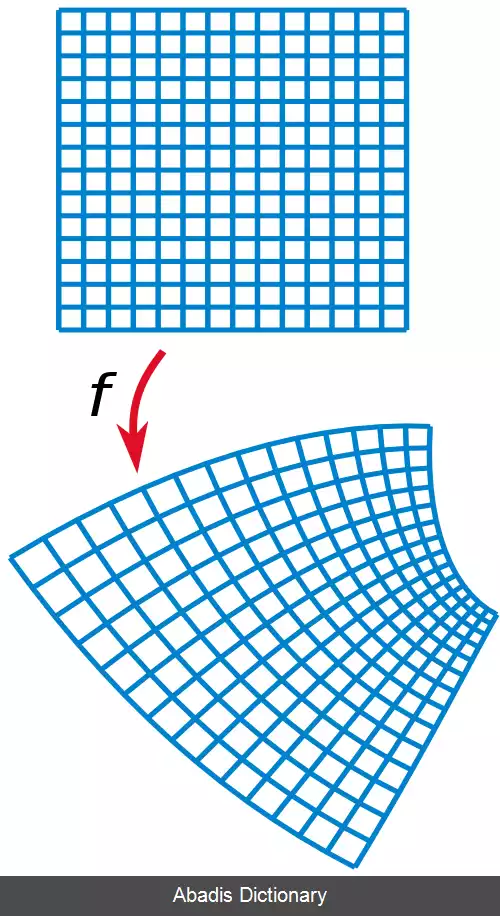
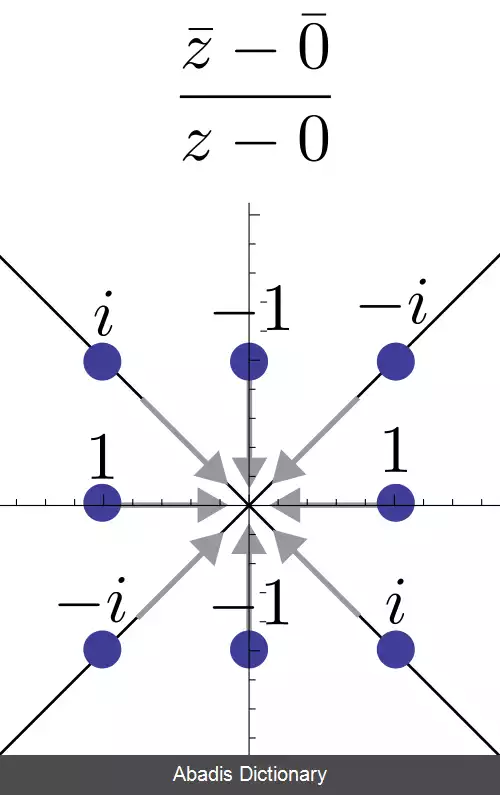
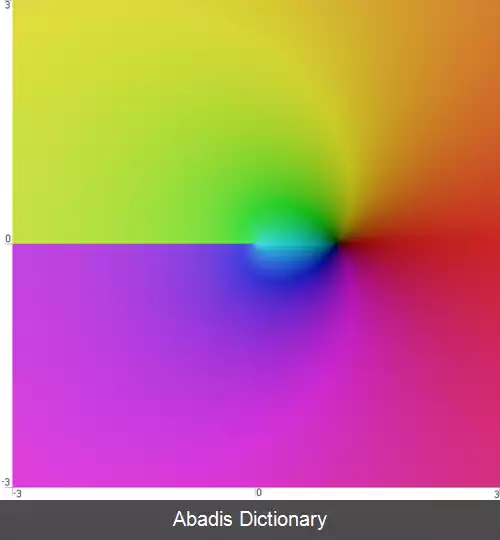
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاگرچه اصطلاح تابع تحلیلی را اغلب بجای اصطلاح «تابع هولومورفیک» بکار می رود، واژه «تحلیلی» به صورت کلی تر تعریف شده است تا به هر تابعی ( حقیقی، مختلط، یا نوع کلی تر ) اشاره کند که آن تابع را باید بتوان بصورت یک سری توانی همگرا در همسایگی هر نقطه در دامنه اش نوشت. این موضوع که همه توابع هولومورفیک نوعی تابع تحلیلی مختلط هستند و برعکس، یک قضیه اصلی در تحلیل مختلط است. [ ۱]
به توابع هولومورفیک گاهی توابع منظم هم می گویند. [ ۲] [ ۳] به تابع هولومورفیکی که دامنه اش کل صفحه مختلط است، یک تابع تام گفته می شود. عبارت «هولومورفیک در یک نقطه z0» فقط به معنی مشتق پذیر در z0 نیست، بلکه به معنی آن است که در همه جا در همسایگی z0 در صفحه مختلط مشتق پذیر است.
اگر به ما یک تابع مختلط - مقدار از یک متغیر منفرد مختلط داده شده باشد، مشتق در یک نقطه z0 در دامنه اش توسط حد زیر تعریف می شود:[ ۴]
این مشابه تعریف مشتق برای توابع حقیقی است، فقط همه کمیت هایش مختلط هستند. بخصوص، حد موقعی گرفته می شود که عدد مختلط z به سمت z0 میل می کند، و باید برای هر دنباله مقادیر مختلط برای z که در صفحه مختلط به سمت z0 میل می کند، مقدار یکسانی داشته باشد. اگر حد موجود باشد، می گوییم که در نقطه z0 مشتق پذیر مختلط است. مفهوم مشتق پذیری مختلط ویژگی های مشترک زیادی با مشتق پذیری حقیقی دارد: خطی است و از قاعده ضرب، قاعده خارج قسمت، و قاعده زنجیره ای پیروی می کند. [ ۵]
اگر در هر نقطه z0 در یک مجموعه باز U مشتق پذیر مختلط باشد، آنوقت می گوییم که روی U هولومورفیک است. می گوییم که در نقطه z0 هرلومورفیک است اگر روی یک همسایگی z0 مشتق پذیر مختلط باشد. [ ۶] می گوییم که روی یک مجموعه غیر - باز A هولومورفیک است اگر روی یک همسایگی A هولومورفیک باشد. به عنوان یک غیر مثال، تابع f ( z ) = | z |2 دقیقا روی یک نقطه ( z0 = 0 ) مشتق پذیر مختلط نیست، و به این دلیل، در نقطه 0 هولومورفیک نیست، زیرا هیچ مجموعه بازی حول 0 موجود نیست که در آن مشتق پذیر مختلط باشد.




wiki: تابع هولومورفیک
