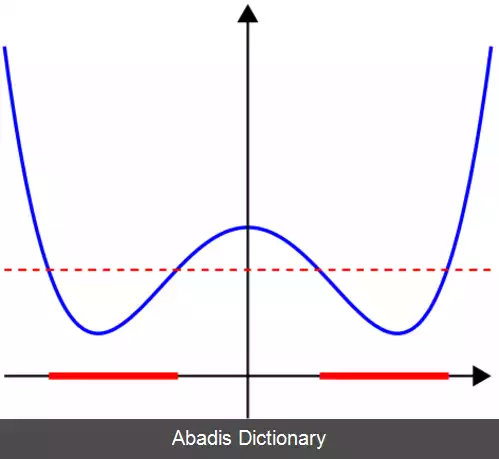
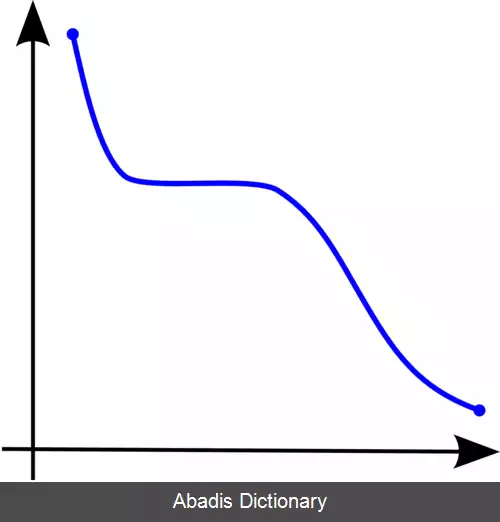
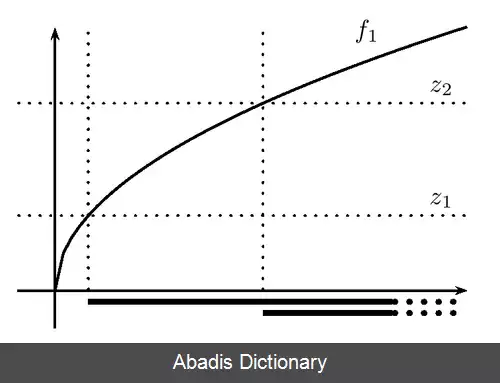
در ریاضیات تابع شبه کوژ یا تابع شبه محدب به تابعی گفته می شود که کلیهٔ مجموعه های سطوح زیرین آن مجموعهٔ کوژ باشند. [ ۱] به زبان ساده تر در یک تابع شبه کوژ، بیشینهٔ تابع روی هر بازهٔ دلخواه از دامنهٔ آن یکی از نقاط ابتدایی یا انتهایی بازه است.
هر تابع شبه کوژی لزوماً کوژ نیست، اما همهٔ توابع کوژ، شبه کوژ هستند.
به بیان ریاضی اگر f : S → R روی مجموعهٔ کوژ S تعریف شده باشد، آنگاه f یک تابع شبه کوژ است اگر به ازای هر x , y ∈ S و λ ∈ داشته باشیم:[ ۲]
در صورتی که در این نابرابری به جای ≤ از < استفاده شود، تعریف تابع اکیداً شبه کوژ به دست می آید.
• منفی یک تابع شبه کوژ یک تابع شبه کاو است.
• هر کمینهٔ موضعی یک تابع شبه کوژ، کمینهٔ سراسری آن نیز هست، اما لزوماً منحصر به فرد نیست. [ ۳]
• اگر f {\displaystyle f} یک تابع شبه کوژ تعریف شده روی مجموعهٔ کوژِ S ⊆ ℜ n {\displaystyle S\subseteq \Re ^{n}} باشد و S ∗ {\displaystyle S^{*}} مجموعهٔ کلیهٔ نقاط کمینهٔ سراسری f {\displaystyle f} ، آنگاه S ∗ {\displaystyle S^{*}} یک مجموعهٔ کوژ است. [ ۴]
توابع شبه کوژ در بررسی نظریه های تصمیم گیری اقتصادی کاربرد دارند. [ ۵]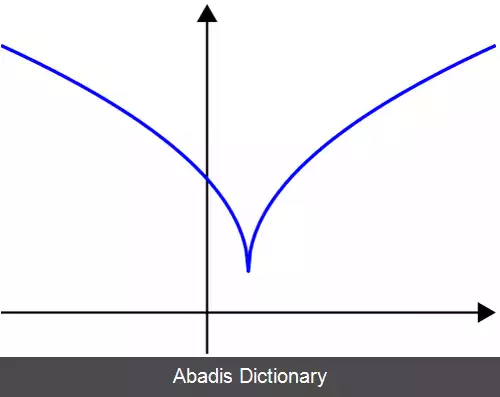
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفهر تابع شبه کوژی لزوماً کوژ نیست، اما همهٔ توابع کوژ، شبه کوژ هستند.
به بیان ریاضی اگر f : S → R روی مجموعهٔ کوژ S تعریف شده باشد، آنگاه f یک تابع شبه کوژ است اگر به ازای هر x , y ∈ S و λ ∈ داشته باشیم:[ ۲]
در صورتی که در این نابرابری به جای ≤ از < استفاده شود، تعریف تابع اکیداً شبه کوژ به دست می آید.
• منفی یک تابع شبه کوژ یک تابع شبه کاو است.
• هر کمینهٔ موضعی یک تابع شبه کوژ، کمینهٔ سراسری آن نیز هست، اما لزوماً منحصر به فرد نیست. [ ۳]
• اگر f {\displaystyle f} یک تابع شبه کوژ تعریف شده روی مجموعهٔ کوژِ S ⊆ ℜ n {\displaystyle S\subseteq \Re ^{n}} باشد و S ∗ {\displaystyle S^{*}} مجموعهٔ کلیهٔ نقاط کمینهٔ سراسری f {\displaystyle f} ، آنگاه S ∗ {\displaystyle S^{*}} یک مجموعهٔ کوژ است. [ ۴]
توابع شبه کوژ در بررسی نظریه های تصمیم گیری اقتصادی کاربرد دارند. [ ۵]





wiki: تابع شبه محدب
