تابع سیگموئید یا سیگماوار ( به انگلیسی: Sigmoid function ) تابعی حقیقی، یکنوا، کران دار و مشتق پذیر است که به ازای کلیه مقادیر حقیقی قابل تعریف بوده دارای مشتق نامنفی است[ ۱] که دارای یک نقطه ی عطف است. این تابع به لحاظ گرافیکی شکلی شبیه حرف S انگلیسی و سیگما در یونانی دارد و دارای رابطه کلی زیر است:[ ۱]
دامنه توابع سیگموئید شامل تمامی اعداد حقیقی بوده و مقدار بازگشتی این تابع نیز به طور یکنواخت از 0 تا 1 یا باتوجه به نوع تابع از 1 تا 1 - تغییر می کند. طیف گسترده ای از توابع سیگموئید از جمله توابع لجستیک و هذلولی به عنوان تابع فعال سازی در شبکه های عصبی استفاده می شود. منحنی های سیگموئید نیز در آمار به عنوان توابع توزیع تجمعی مانند انتگرال های چگالی لجستیک، چگالی نرمال و توابع چگالی تی - استیودنت رایج هستند.
تابع سیگموئید لجستیک معکوس پذیر است و معکوس آن تابع لوجیت است.
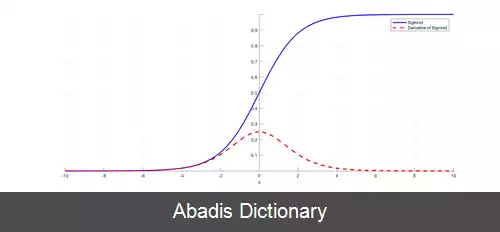
تابع سیگموئید دارای مشتق مرتبه اول است که شکلی مشابه با زنگوله ( bell shaped ) دارد.
تابع سیگموئید برای مقادیر کمتر از یک نقطه خاص شکلی محدب و برای مقادیر بزرگتر از آن نقطه شکلی مقعر دارد.
تابع سیگموئید دارای دو مجانب افقی است:
مشتق این تابع برابر است با:[ ۲]
توابع سیگموئید به چندین شکل و فرم متفاوت وجود دارند و هر یک دارای خصوصیات منحصر به فرد خود می باشند. در زیر به برخی از مهمترین انواع توابع سیگموئید پرداخته شده است:
این تابع شاید معروف ترین شکل تابع سیگموئید باشد و به صورت زیر تعریف می شود:
σ ( x ) = 1 1 + e − x
بر خلاف تابع لجستیک، تابع tanh خروجی هایی بین - 1 و 1 تولید می کند. این تابع به صورت زیر تعریف می شود:
t a n h ( x ) = e x − e − x e x + e − x
این تابع یک نوع دیگر از تابع سیگموئید است که خروجی های بین − π / 2 و π / 2 تولید می کند.
تابع Gompertz یک تابع سیگموئید است که معمولاً در مدل سازی سیستم هایی که رشد اولیه سریع و در ادامه به کندی رشد می کند، مورد استفاده قرار می گیرد. فرمول آن به صورت زیر است:
G o m p e r t z ( x ) = e e − x
این دو تابع اخیراً در حوزه یادگیری عمیق معرفی شده اند. تابع ISRU ( Inverted Square Root Unit ) و ISRLU ( Inverted Square Root Linear Unit ) بر اساس تابع سیگموئید هستند و به ترتیب فرمول زیر را دارند: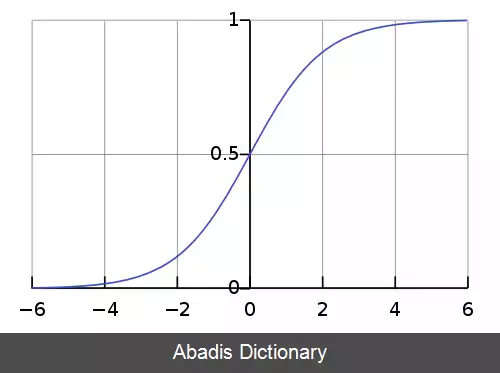
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدامنه توابع سیگموئید شامل تمامی اعداد حقیقی بوده و مقدار بازگشتی این تابع نیز به طور یکنواخت از 0 تا 1 یا باتوجه به نوع تابع از 1 تا 1 - تغییر می کند. طیف گسترده ای از توابع سیگموئید از جمله توابع لجستیک و هذلولی به عنوان تابع فعال سازی در شبکه های عصبی استفاده می شود. منحنی های سیگموئید نیز در آمار به عنوان توابع توزیع تجمعی مانند انتگرال های چگالی لجستیک، چگالی نرمال و توابع چگالی تی - استیودنت رایج هستند.
تابع سیگموئید لجستیک معکوس پذیر است و معکوس آن تابع لوجیت است.
تابع سیگموئید دارای مشتق مرتبه اول است که شکلی مشابه با زنگوله ( bell shaped ) دارد.
تابع سیگموئید برای مقادیر کمتر از یک نقطه خاص شکلی محدب و برای مقادیر بزرگتر از آن نقطه شکلی مقعر دارد.
تابع سیگموئید دارای دو مجانب افقی است:
مشتق این تابع برابر است با:[ ۲]
توابع سیگموئید به چندین شکل و فرم متفاوت وجود دارند و هر یک دارای خصوصیات منحصر به فرد خود می باشند. در زیر به برخی از مهمترین انواع توابع سیگموئید پرداخته شده است:
این تابع شاید معروف ترین شکل تابع سیگموئید باشد و به صورت زیر تعریف می شود:
σ ( x ) = 1 1 + e − x
بر خلاف تابع لجستیک، تابع tanh خروجی هایی بین - 1 و 1 تولید می کند. این تابع به صورت زیر تعریف می شود:
t a n h ( x ) = e x − e − x e x + e − x
این تابع یک نوع دیگر از تابع سیگموئید است که خروجی های بین − π / 2 و π / 2 تولید می کند.
تابع Gompertz یک تابع سیگموئید است که معمولاً در مدل سازی سیستم هایی که رشد اولیه سریع و در ادامه به کندی رشد می کند، مورد استفاده قرار می گیرد. فرمول آن به صورت زیر است:
G o m p e r t z ( x ) = e e − x
این دو تابع اخیراً در حوزه یادگیری عمیق معرفی شده اند. تابع ISRU ( Inverted Square Root Unit ) و ISRLU ( Inverted Square Root Linear Unit ) بر اساس تابع سیگموئید هستند و به ترتیب فرمول زیر را دارند:



wiki: تابع سیگموئید
