در علوم رایانه، یک تابع درهم سازی کامل برای مجموعه S تابع هشی است که عناصر مجزا از S را بدون برخورد به مجموعه ای از اعداد صحیح مرتبط می کند. از نظر ریاضی، یک تایع یک به یک است.
توابع هش کامل ممکن است برای پیاده سازی جدول جستجوی با بدترین زمان دسترسی استفاده شود. یک تابع هش کامل دارای بسیاری از کاربردهای مشابه توابع هش دیگر است، با این برتری که نیازی به بررسی مشکل برخورد ندارد. علاوه بر این، اگر کلیدها داده نباشند، لازم نیست کلیدها در جدول جستجو ذخیره شوند و موجب صرفه جویی در حافظه می شوند.
با قرار دادن کلیدهای S ( یا سایر مقادیر مرتبط ) در یک جدول جستجوی فهرست شده ( با اندیس ) بوسیله خروجی این تابع، یک تابع درهم سازی کامل با مقادیر محدود می تواند برای یه عملیات جست و جوی کارآمد استفاده شود. سپس می توان با جستجوی سلول کلید مورد نظر در جدول، وجود کلید در S را آزمایش کرد یا مقدار متناظر با آن را جستجو کرد. هرگونه جستجو در بدترین حالت در زمان ثابت صورت می گیرد. [ ۱]
یک تابع درهم سازی کامل برای یک مجموعه خاص S می تواند در زمان ثابت تعیین شود. یا با مقادیر موجود در یک محدوده کوچک، توسط یک الگوریتم تصادفی در تعدادی از عملیات ها که ( که تعداد آن متناسب با اندازه S می باشد ) می تواند جستجو شود. روش ساختن ( Fredman، Komlós و Szemerédi 1984 ) از یک طرح دو سطحی استفاده می کند تا یک مجموعه S از n عنصر به طیف وسیعی از O ( n ) شاخص مرتبط ( نقشه ) کند، و پس از آن هر شاخص به طیف وسیعی از مقادیر هش مرتبط می شود. سطح اول ساخت آنها، یک p اول بسیار بزرگ ( بزرگتر از اندازه مجموعه ای که S از آن ترسیم شده است ) ، و یک پارامتر k انتخاب می کند و هر عنصر x از S را به نمایه ( اندیس ) خودش مرتبط می کند.
اگر k به طور تصادفی انتخاب شود، این مرحله به احتمال زیاد دچار برخورد می شود، اما تعداد عناصر ni که همزمان به همان اندیس i مرتبط ( هش ) می شوند، احتمالاً اندک است. در سطح دوم ساخت آن به هر اندیس یا شاخص i دامنه O ( ni2 ) از اعداد صحیح را مرتبط می کند. سطح دوم از یک مجموعه دومی شامل توابع ماژولار خطی برای هر اندیس i استفاده می کند تا هر عضو x از S را به محدودهg ( x ) مرتبط می کند. [ ۱]
( Fredman، Komlós و Szemerédi 1984 ) نشان می دهند ، انتخابی برای k وجود دارد طوری که مجموع طول دامنه ها برای n مقدار متفاوت ( g ( x برابر ( O ( n باشد. همچنین، برای هر مقدار g ( x ) ، یک تابع ماژولار خطی وجود دارد که زیر مجموعهٔ مطابقت یافته S را با محدوده مربوط به آن مقدار مرتبط می کند. چه توابع سطح دوم چه k به ازای هر مقدار g ( x ) با انتخاب مقادیر تصادفی تا زمانی که یکی از آنها را بیابد می تواند در زمان چند جمله ای کار کند. [ ۱]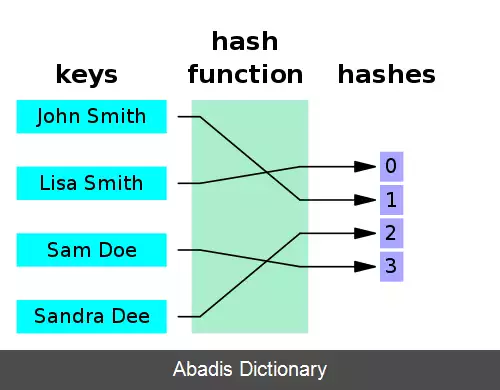

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفتوابع هش کامل ممکن است برای پیاده سازی جدول جستجوی با بدترین زمان دسترسی استفاده شود. یک تابع هش کامل دارای بسیاری از کاربردهای مشابه توابع هش دیگر است، با این برتری که نیازی به بررسی مشکل برخورد ندارد. علاوه بر این، اگر کلیدها داده نباشند، لازم نیست کلیدها در جدول جستجو ذخیره شوند و موجب صرفه جویی در حافظه می شوند.
با قرار دادن کلیدهای S ( یا سایر مقادیر مرتبط ) در یک جدول جستجوی فهرست شده ( با اندیس ) بوسیله خروجی این تابع، یک تابع درهم سازی کامل با مقادیر محدود می تواند برای یه عملیات جست و جوی کارآمد استفاده شود. سپس می توان با جستجوی سلول کلید مورد نظر در جدول، وجود کلید در S را آزمایش کرد یا مقدار متناظر با آن را جستجو کرد. هرگونه جستجو در بدترین حالت در زمان ثابت صورت می گیرد. [ ۱]
یک تابع درهم سازی کامل برای یک مجموعه خاص S می تواند در زمان ثابت تعیین شود. یا با مقادیر موجود در یک محدوده کوچک، توسط یک الگوریتم تصادفی در تعدادی از عملیات ها که ( که تعداد آن متناسب با اندازه S می باشد ) می تواند جستجو شود. روش ساختن ( Fredman، Komlós و Szemerédi 1984 ) از یک طرح دو سطحی استفاده می کند تا یک مجموعه S از n عنصر به طیف وسیعی از O ( n ) شاخص مرتبط ( نقشه ) کند، و پس از آن هر شاخص به طیف وسیعی از مقادیر هش مرتبط می شود. سطح اول ساخت آنها، یک p اول بسیار بزرگ ( بزرگتر از اندازه مجموعه ای که S از آن ترسیم شده است ) ، و یک پارامتر k انتخاب می کند و هر عنصر x از S را به نمایه ( اندیس ) خودش مرتبط می کند.
اگر k به طور تصادفی انتخاب شود، این مرحله به احتمال زیاد دچار برخورد می شود، اما تعداد عناصر ni که همزمان به همان اندیس i مرتبط ( هش ) می شوند، احتمالاً اندک است. در سطح دوم ساخت آن به هر اندیس یا شاخص i دامنه O ( ni2 ) از اعداد صحیح را مرتبط می کند. سطح دوم از یک مجموعه دومی شامل توابع ماژولار خطی برای هر اندیس i استفاده می کند تا هر عضو x از S را به محدودهg ( x ) مرتبط می کند. [ ۱]
( Fredman، Komlós و Szemerédi 1984 ) نشان می دهند ، انتخابی برای k وجود دارد طوری که مجموع طول دامنه ها برای n مقدار متفاوت ( g ( x برابر ( O ( n باشد. همچنین، برای هر مقدار g ( x ) ، یک تابع ماژولار خطی وجود دارد که زیر مجموعهٔ مطابقت یافته S را با محدوده مربوط به آن مقدار مرتبط می کند. چه توابع سطح دوم چه k به ازای هر مقدار g ( x ) با انتخاب مقادیر تصادفی تا زمانی که یکی از آنها را بیابد می تواند در زمان چند جمله ای کار کند. [ ۱]


wiki: تابع درهم سازی کامل
