یک تابع جزئی از X به Y ( که به صورت f: X ↛ Y یا f: X ⇸ Y نوشته می شود ) ، تابع f: X ′ → Y برای یک زیرمجموعه سره X ′ از X است. اگر زیرمجموعهٔ X ′ سره نباشد ( یعنی اگر X ′ = X ) تابع f یک تابع کامل است. از توابع جزئی معمولاً زمانی استفاده می شود که دامنه یک تابع مشخص نیست ( مثلاً بسیاری از توابع در نظریه رایانش پذیری این گونه هستند ) .
به طور خاص، گفته می شود برای هر x ∈ X یا:
• f ( x ) = y ∈ Y ( تابع به عنوان یک عضو مفرد از Y تعریف شده است ) و یا
• f ( x ) تعریف نشده است.
برای مثال، تابع ریشه دوم تنها محدود به اعداد صحیح است:
بنابراین تابع g ( n ) تنها برای nهایی تعریف می شود که مربع کامل باشند ( مثلاً ۰, ۱, ۴, ۹, ۱۶, . . . ) . یعنی g ( 25 ) = ۵، ولی g ( 26 ) تعریف نشده است.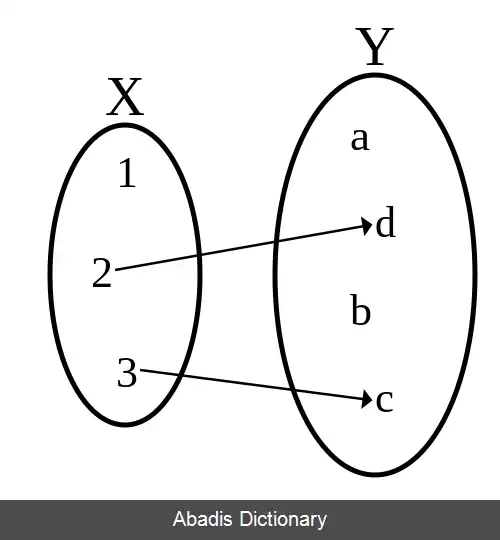
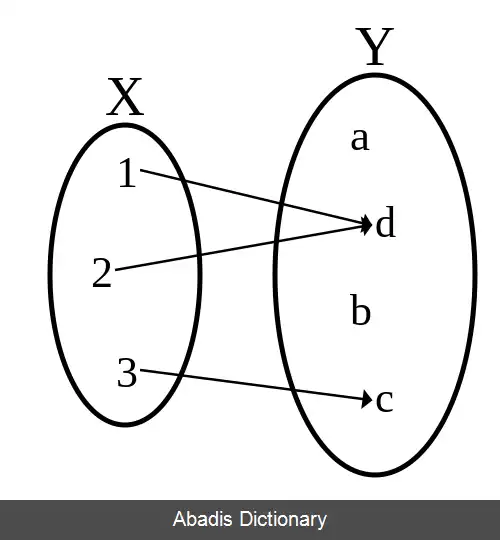
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبه طور خاص، گفته می شود برای هر x ∈ X یا:
• f ( x ) = y ∈ Y ( تابع به عنوان یک عضو مفرد از Y تعریف شده است ) و یا
• f ( x ) تعریف نشده است.
برای مثال، تابع ریشه دوم تنها محدود به اعداد صحیح است:
بنابراین تابع g ( n ) تنها برای nهایی تعریف می شود که مربع کامل باشند ( مثلاً ۰, ۱, ۴, ۹, ۱۶, . . . ) . یعنی g ( 25 ) = ۵، ولی g ( 26 ) تعریف نشده است.


wiki: تابع جزئی
