در هندسهٔ تحلیلی، بیضی گون[ ۱] [ ۲] [ ۳] ( به انگلیسی: Ellipsoid ) یا بیضی وار[ ۴] یک رویهٔ کران دار و یکی از انواع رویه های درجهٔ دوم است. [ ۵] بیضی گون را می توان حاصل دِفُرمه کردن یک کره تصور کرد.
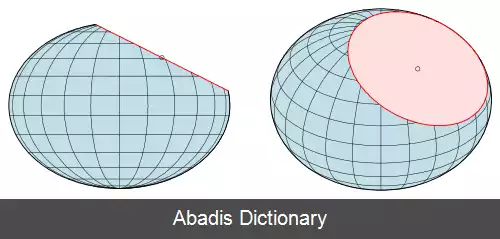
هر سطح مقطع از بیضی گون یا یک بیضی است، یا یک نقطه یا تهی. [ ۶] به همین دلیل است که بیضی گون ( به معنی شبیه بیضی ) نامگذاری شده.
بیضی گون سه محور ( خط ) تقارن دارد که همگی برهم عمود و در یک مرکز ( نقطه ) تقارن ( مرکز بیضی ) با یکدیگر متقاطع هستند.
سه پاره خط محدود در بیضی و روی محورهای تقارنش را قطرهای بیضی می نامند.
حجم بیضی گون به کمک فرمول 4 3 π a b c زیر به دست می آید.
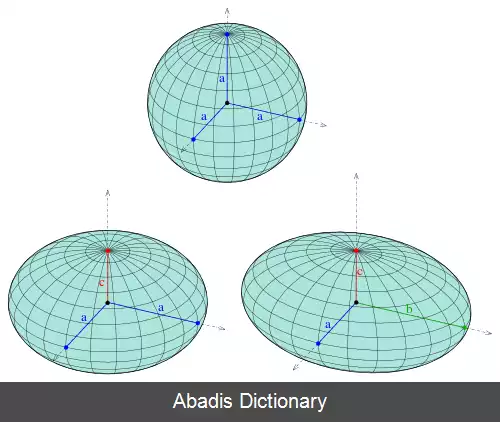
• اگر دو تا از قطرهای بیضی گون برابر باشند، به آن کره وار نیز می گویند که از دوران یک بیضی به دست می آید.
• اگر هر سه قطر بیضی با یکدیگر برابر باشند، به آن کره می گویند.
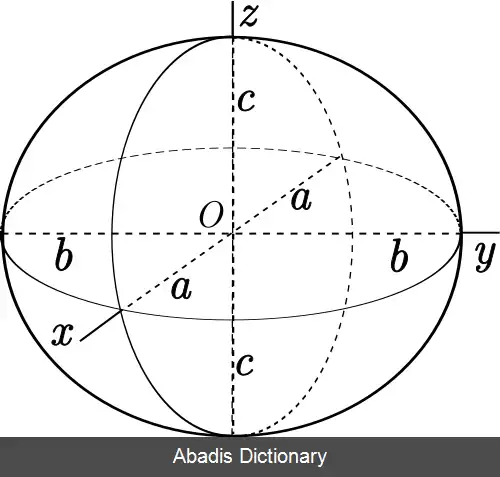
در دستگاه مختصات دکارتی، روش استاندارد نمایش بیضی گون با قطرهای 2 a و 2 b و 2 c و با مرکز در مبدأ مختصات به صورت زیر است:[ ۵]
x 2 a 2 + y 2 b 2 + z 2 c 2 = 1
بیضی گون یک رویهٔ درجه دو است. یک ابربیضی گون در فضای R n ، یک ابررویهٔ درجه دو است.
یک ابربیضی گون با مرکز در مبدأ مختصات شعاع های c 1 , c 2 , … , c n ، مکان هندسی نقاطی مانند P = ( x 1 , x 2 , … , x n ) است که در معادلهٔ استاندارد زیر صدق کنند:
x 1 2 c 1 2 + x 2 2 c 2 2 + ⋯ + x n 2 c n 2 = 1
محاسبهٔ حجم ابربیضی گون شبیه بیضی گون است.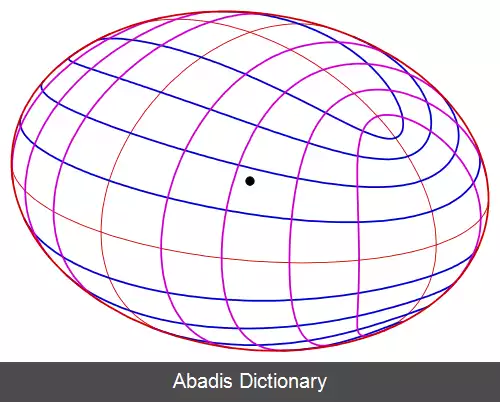
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفهر سطح مقطع از بیضی گون یا یک بیضی است، یا یک نقطه یا تهی. [ ۶] به همین دلیل است که بیضی گون ( به معنی شبیه بیضی ) نامگذاری شده.
بیضی گون سه محور ( خط ) تقارن دارد که همگی برهم عمود و در یک مرکز ( نقطه ) تقارن ( مرکز بیضی ) با یکدیگر متقاطع هستند.
سه پاره خط محدود در بیضی و روی محورهای تقارنش را قطرهای بیضی می نامند.
حجم بیضی گون به کمک فرمول 4 3 π a b c زیر به دست می آید.
• اگر دو تا از قطرهای بیضی گون برابر باشند، به آن کره وار نیز می گویند که از دوران یک بیضی به دست می آید.
• اگر هر سه قطر بیضی با یکدیگر برابر باشند، به آن کره می گویند.
در دستگاه مختصات دکارتی، روش استاندارد نمایش بیضی گون با قطرهای 2 a و 2 b و 2 c و با مرکز در مبدأ مختصات به صورت زیر است:[ ۵]
x 2 a 2 + y 2 b 2 + z 2 c 2 = 1
بیضی گون یک رویهٔ درجه دو است. یک ابربیضی گون در فضای R n ، یک ابررویهٔ درجه دو است.
یک ابربیضی گون با مرکز در مبدأ مختصات شعاع های c 1 , c 2 , … , c n ، مکان هندسی نقاطی مانند P = ( x 1 , x 2 , … , x n ) است که در معادلهٔ استاندارد زیر صدق کنند:
x 1 2 c 1 2 + x 2 2 c 2 2 + ⋯ + x n 2 c n 2 = 1
محاسبهٔ حجم ابربیضی گون شبیه بیضی گون است.




wiki: بیضی گون
