در ریاضیات و جبر مقدماتی، قضیهٔ بسط دو جمله ای ( به انگلیسی: Binomial theorem or binomial expansion ) گسترش جبری توانهای دو جمله ای را توصیف می کند. بنا بر این قضیه؛ می توان چندجمله ای های ( x + y ) n را به صورت a xb yc گسترش داد: در حالی که b و c اعداد حسابیِ غیر انتزاعی هستند و نیز ، b + c = n و ضریب a خود یک عدد صحیح مثبت است، و به n و b وابسته است.
فرمولها برای محاسبهٔ توانهای دو جمله ای هایی - مثلاً برای 2 < = n < = 5 به این صورت آمده اند:
هدف این است که فرمولی برای ( x + y ) n که در آن n عدد طبیعی است بدست آوریم. در این جا قضیه دو جمله ای را بیان و ثابت می کنیم.
اگر n عدد طبیعی باشد، آنگاه
که: ( n k ) = n ! k ! ( n − k ) ! ضریب دوجمله ای است و !n فاکتوریل n را بیان می کند. این فرمول و آرایش مثلثی ضرایب ثابت دو جمله ای که به مثلث پاسکال نسبت داده می شود ( کسی که در قرن هفدهم آنها را توصیف کرده اما اینها توسط ریاضیدانان زیادی زودتر از او کشف شده بود در قرن یازدهم توسط عمر خیام ریاضیدان ایرانی، در قرن سیزدهم توسط یانگ هو ریاضیدان چینی )
در این جا همهٔ x و yهای حقیقی و مختلط صدق می کند و به طور کلی تر برای مقادیر x و y به طوری که xy=yx باشد
یک روش برای اثبات قضیه دو جمله ای، استقرای ریاضی است وقتی که n = ۰ است ما داریم
برای گام استقرا فرض می کنیم که قضیه برای m درست، آنگاه n = m + 1
یک عدد از فرم x n ± y n بدست می آید یک عدد دو جمله ای است که n نا منفی یا فرد است وقتی که n منفی یا فرد است می توان از این اعداد فاکتورگیری کرد
برای بسط دادن دو جمله ای های به فرم: ( x + y ) n
عبارت اول: x n است و ضریب ثابت عبارت بعدی برابراست با ضرب ضریب ثابت فعلی در توان x تقسیم بر تعداد عبارت موجود، توان x کاهش و توان y افزایش میابد تا این که توان x به صفر و توان y به n برسد
برای مثال:
عبارت اول: x 10
برای یافتن ضریب دومین عبارت: ضرب ۱ ( ضریب ثابت فعلی ) در ۱۰ ( توان فعلی x ) و تقسیم بر تعداد عبارت موجود ( ۱، چون یک عبارت وجود دارد ) پس حاصل ۱۰ بدست می آید: 10 x 9 y
به همین شکل ضریب ثابت بعدی ۲/ ( ۱۰×۹ ) و به همین روش ادامه می دهیم تا اینکه توان y برابر ۱۰ و توان x برابر صفر شود
متوجه می شوید که ضرایب ثابت متقارن هستند این زمانی اتفاق می افتد که ضرایب ثابت x و y در پرانتز عبارت اصلی یکی باشند پی بردن به این نکته می تواند در صرفه جویی در وقت کمک کند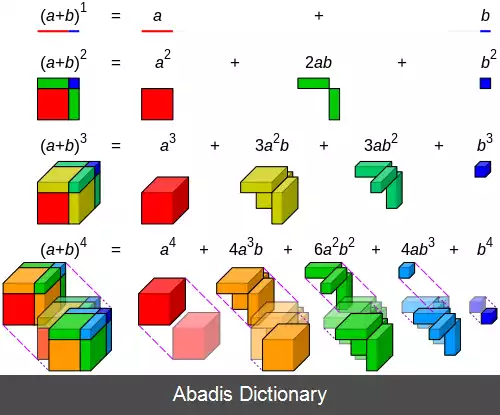

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرمولها برای محاسبهٔ توانهای دو جمله ای هایی - مثلاً برای 2 < = n < = 5 به این صورت آمده اند:
هدف این است که فرمولی برای ( x + y ) n که در آن n عدد طبیعی است بدست آوریم. در این جا قضیه دو جمله ای را بیان و ثابت می کنیم.
اگر n عدد طبیعی باشد، آنگاه
که: ( n k ) = n ! k ! ( n − k ) ! ضریب دوجمله ای است و !n فاکتوریل n را بیان می کند. این فرمول و آرایش مثلثی ضرایب ثابت دو جمله ای که به مثلث پاسکال نسبت داده می شود ( کسی که در قرن هفدهم آنها را توصیف کرده اما اینها توسط ریاضیدانان زیادی زودتر از او کشف شده بود در قرن یازدهم توسط عمر خیام ریاضیدان ایرانی، در قرن سیزدهم توسط یانگ هو ریاضیدان چینی )
در این جا همهٔ x و yهای حقیقی و مختلط صدق می کند و به طور کلی تر برای مقادیر x و y به طوری که xy=yx باشد
یک روش برای اثبات قضیه دو جمله ای، استقرای ریاضی است وقتی که n = ۰ است ما داریم
برای گام استقرا فرض می کنیم که قضیه برای m درست، آنگاه n = m + 1
یک عدد از فرم x n ± y n بدست می آید یک عدد دو جمله ای است که n نا منفی یا فرد است وقتی که n منفی یا فرد است می توان از این اعداد فاکتورگیری کرد
برای بسط دادن دو جمله ای های به فرم: ( x + y ) n
عبارت اول: x n است و ضریب ثابت عبارت بعدی برابراست با ضرب ضریب ثابت فعلی در توان x تقسیم بر تعداد عبارت موجود، توان x کاهش و توان y افزایش میابد تا این که توان x به صفر و توان y به n برسد
برای مثال:
عبارت اول: x 10
برای یافتن ضریب دومین عبارت: ضرب ۱ ( ضریب ثابت فعلی ) در ۱۰ ( توان فعلی x ) و تقسیم بر تعداد عبارت موجود ( ۱، چون یک عبارت وجود دارد ) پس حاصل ۱۰ بدست می آید: 10 x 9 y
به همین شکل ضریب ثابت بعدی ۲/ ( ۱۰×۹ ) و به همین روش ادامه می دهیم تا اینکه توان y برابر ۱۰ و توان x برابر صفر شود
متوجه می شوید که ضرایب ثابت متقارن هستند این زمانی اتفاق می افتد که ضرایب ثابت x و y در پرانتز عبارت اصلی یکی باشند پی بردن به این نکته می تواند در صرفه جویی در وقت کمک کند


wiki: بسط دوجمله ای
