در ریاضیات بستار تعدی یک رابطه دوتایی R در مجموعه X، کوچکترین رابطه از X، شامل R که متعدی باشد.
برای مثال اگر X یک مجموعه ای از فرودگاه ها و x R y به معنی "یک پرواز مستقیم از فرودگاه x به فرودگاه y وجود دارد" ( برای x و y در X ) باشد، سپس بستار تعدی R در X، رابطه R+ است به طوری که x R+ y به معنی آن است که "ممکن است برای پرواز از x به y یک یا چند پرواز انجام شود". به عبارت دیگر بستار تعدی مجموعه ای از تمام نقاطی را به شما می دهد که می توانید از هر نقطهٔ شروع به آن ها برسید.
به صورت دقیق تر، بستار تعدی رابطه باینری R در مجموعه X، کوچکترین رابطه متعدی روی مجموعه X است به طوری که R+ شامل R باشد ( ( Lidl و Pilz 1998، ص. ۳۳۷ ) ) . اگر رابطهٔ دودویی به خودی خود متعدی باشد بسطار تعدی آن خود رابطه می شود؛ در غیر این صورت بستار تعدی رابطه ای دیگر می شود.
رابطه R در مجموعه X متعدی است، اگر برای تمام x و y و zهای موجود در Xکه x R y و y R z ، نتیجه بدهد x R z. نمونه هایی از روابط متعدی عبارتند از:
رابطهٔ برابری در هر مجموعه ای، رابطهٔ "کوچکتر یا مساوی " در هر مجموعهٔ مرتب خطی، و رابطهٔ "x قبل از y متولد شده" در مجموعهٔ همه مردم. این روابط را می توان به صورت نمادین نشان داد: اگر x < y و y < z آنگاه x < z است.
یک مثال از یک رابطهٔ غیر متعدی:
«میتوان از شهر y با پرواز مستقیم به شهر x رسید» در مجموعهٔ تمام شهرها.
تنها به دلیل وجود یک پرواز مستقیم از شهری به شهر دوم و یک پرواز مستقیم از شهر دوم به سوم، پرواز مستقیم از شهر اول به شهر دوم وجود ندارد. بستار تعدی این رابطه متفاوت است، یعنی «دنباله ای از پروازهای مستقیم که در شهر X شروع می شود و در شهر y به پایان می رسد». هر رابطه ای را می توان بسط داد در یک روش مشابه به یک رابطهٔ متعدی.
به عنوان مثال یک رابطهٔ غیر تعدی که نسبت به تعدی بودن بسته نیست «روز x بعد از روز y در هفته هست».
این بستار تعدی این رابطه است:
"چند روز x می آید بعد از y"
که بدیهی است برای تمام روزهای هفته x و y ( این معادل یک دستگاه دکارتی است که"x , y روزهای هفته اند" )
برای هر رابطه R، بستار تعدی R همیشه وجود دارد. برای دیدن این، توجه داشته باشید که اشتراک هر خانواده از روابط متعدی، متعدی است.
بعلاوه حداقل یک رابطه متعدی حاوی R وجود دارد از جمله: X × X. بستار تعدی R اشتراک همه روابط متعدی حاوی رابطهٔ R است.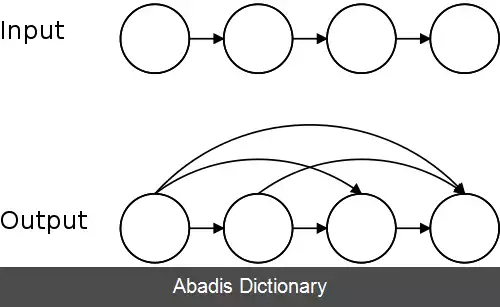
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبرای مثال اگر X یک مجموعه ای از فرودگاه ها و x R y به معنی "یک پرواز مستقیم از فرودگاه x به فرودگاه y وجود دارد" ( برای x و y در X ) باشد، سپس بستار تعدی R در X، رابطه R+ است به طوری که x R+ y به معنی آن است که "ممکن است برای پرواز از x به y یک یا چند پرواز انجام شود". به عبارت دیگر بستار تعدی مجموعه ای از تمام نقاطی را به شما می دهد که می توانید از هر نقطهٔ شروع به آن ها برسید.
به صورت دقیق تر، بستار تعدی رابطه باینری R در مجموعه X، کوچکترین رابطه متعدی روی مجموعه X است به طوری که R+ شامل R باشد ( ( Lidl و Pilz 1998، ص. ۳۳۷ ) ) . اگر رابطهٔ دودویی به خودی خود متعدی باشد بسطار تعدی آن خود رابطه می شود؛ در غیر این صورت بستار تعدی رابطه ای دیگر می شود.
رابطه R در مجموعه X متعدی است، اگر برای تمام x و y و zهای موجود در Xکه x R y و y R z ، نتیجه بدهد x R z. نمونه هایی از روابط متعدی عبارتند از:
رابطهٔ برابری در هر مجموعه ای، رابطهٔ "کوچکتر یا مساوی " در هر مجموعهٔ مرتب خطی، و رابطهٔ "x قبل از y متولد شده" در مجموعهٔ همه مردم. این روابط را می توان به صورت نمادین نشان داد: اگر x < y و y < z آنگاه x < z است.
یک مثال از یک رابطهٔ غیر متعدی:
«میتوان از شهر y با پرواز مستقیم به شهر x رسید» در مجموعهٔ تمام شهرها.
تنها به دلیل وجود یک پرواز مستقیم از شهری به شهر دوم و یک پرواز مستقیم از شهر دوم به سوم، پرواز مستقیم از شهر اول به شهر دوم وجود ندارد. بستار تعدی این رابطه متفاوت است، یعنی «دنباله ای از پروازهای مستقیم که در شهر X شروع می شود و در شهر y به پایان می رسد». هر رابطه ای را می توان بسط داد در یک روش مشابه به یک رابطهٔ متعدی.
به عنوان مثال یک رابطهٔ غیر تعدی که نسبت به تعدی بودن بسته نیست «روز x بعد از روز y در هفته هست».
این بستار تعدی این رابطه است:
"چند روز x می آید بعد از y"
که بدیهی است برای تمام روزهای هفته x و y ( این معادل یک دستگاه دکارتی است که"x , y روزهای هفته اند" )
برای هر رابطه R، بستار تعدی R همیشه وجود دارد. برای دیدن این، توجه داشته باشید که اشتراک هر خانواده از روابط متعدی، متعدی است.
بعلاوه حداقل یک رابطه متعدی حاوی R وجود دارد از جمله: X × X. بستار تعدی R اشتراک همه روابط متعدی حاوی رابطهٔ R است.

wiki: بستار تعدی
