در فیزیک، بسامد زاویه ای ω ( امگا ) به اندازهٔ عددی سرعت چرخش گفته می شود. بسامد زاویه ای برابر با بزرگی بردار سرعت زاویه ای است.
هر دور چرخش برابر است با ۲π رادیان؛ از این رو:
که در آن:
بسامد زاویه ای تنها مضربی از بسامد معمولی است. با این حال کاربرد بسامد زاویه ای در بیشتر برنامه های کاربردی مانند حرکت ساده همساز ( برای دوری از عدد π ) ترجیح داده می شود. در واقع این کمیت در بسیاری از رشته های فیزیک شامل پدیده های تناوبی مانند مکانیک کوانتوم و الکترومغناطیس کلاسیک بکار می رود.
در اس آی بسامد زاویه ای به صورت رادیان بر ثانیه اندازه گرفته می شود. بیاد داشته باشید که هرتز ( Hz ) برای فرکانس معمولی ( f ) بکار می رود نه برای ω.
در حرکت دورانی رابطهٔ بین بسامد زاویه ای، سرعت مماس و فاصله از محور دوران از این قرار است:
• گفتار اصلی نوسانگر هماهنگ
جسم متصل به یک فنر حرکت نوسانی دارد. اگر فنر را ایده آل و جسم آن را صفر در نظر بگیریم، حرکت جسم از قانون نوسانگر هماهنگ ساده پیروی می کند که بسامد زاویه ای آن برابر است با:
شتاب این نوسانگر از رابطهٔ زیر بدست می آید:
که در آن x فاصلهٔ نوسانگر از نقطهٔ تعادل است. این رابطه را همچنین می توان به صورت زیر نوشت:
• گفتار اصلی مدار ال سی
بسامد زاویه ای تشدید شده در مدار ال سی برابرست با ریشه دوم معکوس حاصل ضرب ظرفیت خازن ( C با فاراد اندازه گیری می شود ) در زمان اندوکتانس مدار ( L در هنری )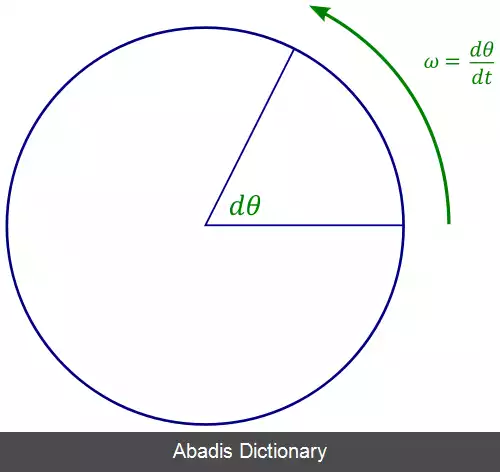
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفهر دور چرخش برابر است با ۲π رادیان؛ از این رو:
که در آن:
بسامد زاویه ای تنها مضربی از بسامد معمولی است. با این حال کاربرد بسامد زاویه ای در بیشتر برنامه های کاربردی مانند حرکت ساده همساز ( برای دوری از عدد π ) ترجیح داده می شود. در واقع این کمیت در بسیاری از رشته های فیزیک شامل پدیده های تناوبی مانند مکانیک کوانتوم و الکترومغناطیس کلاسیک بکار می رود.
در اس آی بسامد زاویه ای به صورت رادیان بر ثانیه اندازه گرفته می شود. بیاد داشته باشید که هرتز ( Hz ) برای فرکانس معمولی ( f ) بکار می رود نه برای ω.
در حرکت دورانی رابطهٔ بین بسامد زاویه ای، سرعت مماس و فاصله از محور دوران از این قرار است:
• گفتار اصلی نوسانگر هماهنگ
جسم متصل به یک فنر حرکت نوسانی دارد. اگر فنر را ایده آل و جسم آن را صفر در نظر بگیریم، حرکت جسم از قانون نوسانگر هماهنگ ساده پیروی می کند که بسامد زاویه ای آن برابر است با:
شتاب این نوسانگر از رابطهٔ زیر بدست می آید:
که در آن x فاصلهٔ نوسانگر از نقطهٔ تعادل است. این رابطه را همچنین می توان به صورت زیر نوشت:
• گفتار اصلی مدار ال سی
بسامد زاویه ای تشدید شده در مدار ال سی برابرست با ریشه دوم معکوس حاصل ضرب ظرفیت خازن ( C با فاراد اندازه گیری می شود ) در زمان اندوکتانس مدار ( L در هنری )

wiki: بسامد زاویه ای
