در ریاضیات، برنامه سازی غیر خطی Nonlinear programming ( NLP ) فرایند حل مسئله بهینه سازی است که در آن برخی از محدودیت ها یا خود تابع هدف غیر خطی است. این مسئله بهینه سازی، یک سیستم از برابری ها و نابرابری ها بر روی مجموعه ای از متغیرهای ناشناخته حقیقی، در یک تابع هدف که باید کمینه یا بیشینه شود.
در این روش تابع هدف به صورت تابع F در نظر گرفته می شود.
این تابع بر زیرمجموعه ای چون X از فضای اقلیدسی تعریف شده است ( پس عناصر X می توانند بردار باشند ) . این زیرمجموعه، توسط قیود به شکل g ( x ) =b تعریف می شود. تابع لاگرانژ در این حالت عبارت خواهد بود از: ( ( L ( x، y ) =F ( x ) +y. ( b - g ( x
شرایط لازم برای حل مسئله را می توان از طریق یافتن نقاط بحرانی تابع لاگرانژ ( ماکزیمم سازی بدون قید ) به دست آورد.
برنامه ریزی مرتبه دوم ( QP ) روشی برای مینیمم سازی توابع مرتبه دوم n متغیره با m محدودیت خطی نامساوی یا مساوی یا هر دو است.
مسائل برنامه ریزی مرتبه دوم ساده ترین فرم مسائل برنامه ریزی غیر خطی با محدودیت نا مساوی می باشد.
این الگوریتم برای محدودیت های خطی اصلاح شده که تابع هدف و محدودیت آن ها غیر خطی است محسوب می شود. در اصل روش محدودیت های خطی یا خطی شده را شامل می شود و متغیر جدید با محدودیت تعریف خواهد شد. بیشتر روش های حل مسائل برنامه ریزی غیر خطی عمومی شامل خطی کردن مسئله و به کار بردن تکنیک برنامه ریزی خطی است که به طور خلاصه مراحل زیر طی می شود.
• به دست آوردن مدل با نقاط عملیاتی و خطی کردن تمام محدودیت های تابع هدف حول نقاط عملیاتی. بطوریکه مسئله به فرم برنامه ریزی خطی تبدیل شود. سپس استفاده از برنامه ریزی خطی برای حل مسئله خطی.
• تکرار روش برنامه ریزی خطی برای رسیدن به جواب مناسب با خطی کردن توابع محدودیت ها و تابع هدف و چنانچه به جواب مناسب نرسید با خطی کردن دوباره محدودیت ها و توابع هدف حول نقطه جدید optimum مسئله پیدا می شود.
در روش های ذکر شده ممکن است روش به همگرایی نرسد و این خود یکی از معایب روش های فوق است به واقع بهترین الگوریتم عمومی حاضر استفاده از الگوریتم گرادیان کاهش یافته عمومی است.
یکی از مسائل پرکاربرد و معمول برای توابع غیر خطی و برنامه سازی غیر خطی مسائل مربوط به بهینه سازی است. مثلاً بهینه سازی هزینه حمل و نقل با انتخاب روش یا روش هایی از میان چندین روش نقل و انتقال است که هرکدام ظرفیت ها و محدودیت های متفاوتی دارند. به عنوان مثال نقل و انتقال نفت خام با انتخاب روش های ترکیبی از خط لوله، تانکر، راه آهن، حمل کننده های دریایی که هرکدام توابع هزینه ای متفاوتی دارند می تواند در نهایت به ما یک تابع غیر خطی از هزینه بدهد.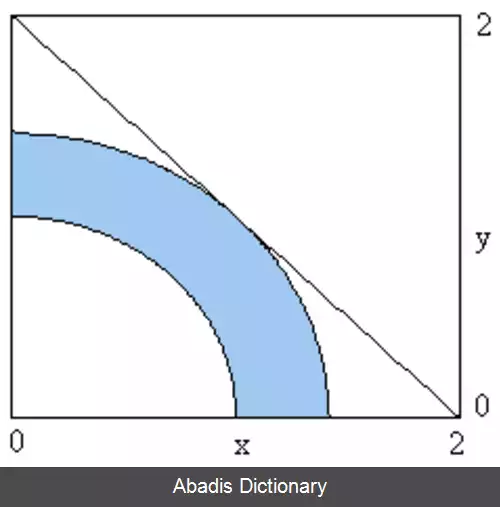
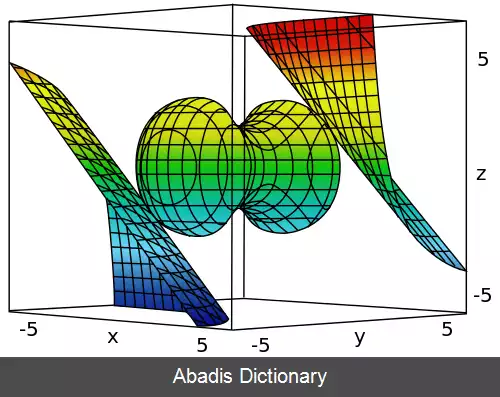
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر این روش تابع هدف به صورت تابع F در نظر گرفته می شود.
این تابع بر زیرمجموعه ای چون X از فضای اقلیدسی تعریف شده است ( پس عناصر X می توانند بردار باشند ) . این زیرمجموعه، توسط قیود به شکل g ( x ) =b تعریف می شود. تابع لاگرانژ در این حالت عبارت خواهد بود از: ( ( L ( x، y ) =F ( x ) +y. ( b - g ( x
شرایط لازم برای حل مسئله را می توان از طریق یافتن نقاط بحرانی تابع لاگرانژ ( ماکزیمم سازی بدون قید ) به دست آورد.
برنامه ریزی مرتبه دوم ( QP ) روشی برای مینیمم سازی توابع مرتبه دوم n متغیره با m محدودیت خطی نامساوی یا مساوی یا هر دو است.
مسائل برنامه ریزی مرتبه دوم ساده ترین فرم مسائل برنامه ریزی غیر خطی با محدودیت نا مساوی می باشد.
این الگوریتم برای محدودیت های خطی اصلاح شده که تابع هدف و محدودیت آن ها غیر خطی است محسوب می شود. در اصل روش محدودیت های خطی یا خطی شده را شامل می شود و متغیر جدید با محدودیت تعریف خواهد شد. بیشتر روش های حل مسائل برنامه ریزی غیر خطی عمومی شامل خطی کردن مسئله و به کار بردن تکنیک برنامه ریزی خطی است که به طور خلاصه مراحل زیر طی می شود.
• به دست آوردن مدل با نقاط عملیاتی و خطی کردن تمام محدودیت های تابع هدف حول نقاط عملیاتی. بطوریکه مسئله به فرم برنامه ریزی خطی تبدیل شود. سپس استفاده از برنامه ریزی خطی برای حل مسئله خطی.
• تکرار روش برنامه ریزی خطی برای رسیدن به جواب مناسب با خطی کردن توابع محدودیت ها و تابع هدف و چنانچه به جواب مناسب نرسید با خطی کردن دوباره محدودیت ها و توابع هدف حول نقطه جدید optimum مسئله پیدا می شود.
در روش های ذکر شده ممکن است روش به همگرایی نرسد و این خود یکی از معایب روش های فوق است به واقع بهترین الگوریتم عمومی حاضر استفاده از الگوریتم گرادیان کاهش یافته عمومی است.
یکی از مسائل پرکاربرد و معمول برای توابع غیر خطی و برنامه سازی غیر خطی مسائل مربوط به بهینه سازی است. مثلاً بهینه سازی هزینه حمل و نقل با انتخاب روش یا روش هایی از میان چندین روش نقل و انتقال است که هرکدام ظرفیت ها و محدودیت های متفاوتی دارند. به عنوان مثال نقل و انتقال نفت خام با انتخاب روش های ترکیبی از خط لوله، تانکر، راه آهن، حمل کننده های دریایی که هرکدام توابع هزینه ای متفاوتی دارند می تواند در نهایت به ما یک تابع غیر خطی از هزینه بدهد.


wiki: برنامه سازی غیرخطی
