برنامه ریزی خطی، یا همان بهینه سازی خطی، روشی در ریاضیات است که به پیدا کردن مقدار کمینه یا بیشینه از یک تابع خطی روی یک چندضلعی ( یا چندوجهی ) محدب می پردازد. [ ۱] این چندضلعی محدب در حقیقت نمایش نموداری تعدادی محدودیت از نوع نامعادله روی متغیرهای تابع است. به بیان ساده تر، به وسیله برنامه سازی خطی می توان بهترین نتیجه ( مثلاً بیشترین سود یا کمترین هزینه ) را در شرایط خاص و با محدودیت های خاص به دست آورد. محل اصلی استفاده برنامه ریزی خطی در مدیریت و اقتصاد است، اما در مهندسی نیز کاربردهای فراوانی دارد. در واقع برنامه ریزی خطی بخشی از برنامه ریزی ریاضی و تحقیق در عملیات موسوم به علم مدیریت است که اولین بار توسط نیروی هوایی ارتش آمریکا بکار گرفته شد. می توان گفت حدود یک چهارم کل محاسبات علمی که بر روی رایانه انجام گرفته است، به برنامه ریزی خطی و مشتقات آن مربوط می شود. [ ۲]
مسئلهٔ حل مجموعه ای از نامعادلات خطی از زمان فوریه مطرح بوده است. برنامه ریزی خطی به عنوان یک مدل ریاضی در زمان جنگ جهانی دوم شکل گرفت تا خرج ها و بازگشت های مالی را طوری سامان بخشد که به کاهش هزینه های ارتش و افزایش خسارات دشمن بینجامد. این طرح تا سال ۱۹۴۷ سری باقی ماند. پس از جنگ، بسیاری از صنایع به استفاده از آن پرداختند. پایه گذاران این حوزه جورج دانتزیگ منتشرکنندهٔ روش سیمپلکس در سال ۱۹۴۷، جان فون نویمان مطرح کننده نظریه دوگانگی در همان سال، و لئونید کانتروویچ ریاضیدان روس که از تکنیک های مشابهی پیش از دانتزینگ استفاده کرد و نوبل سال ۱۹۵۷ را برد هستند. نخستین بار در سال ۱۹۷۹ لئونید خاچیان نشان داد که مسئله برنامه ریزی خطی در مرتبه زمانی چندجمله ای قابل حل است. اما پیشرفت اساسی تر زمانی حاصل شد که نراندرا کارمارکار یک روش نقطه داخلی جدید برای حل این مسائل معرفی کرد. مثال دانتزینگ برای منتصب کردن هفتاد نفر به هفتاد شغل متمایز کارآمدی برنامه ریزی خطی را به نمایش می گذارد. توان محاسباتی لازم برای آزمودن همهٔ جایگشتهای ممکن این مسئله بسیار بالاست. این تعداد از تعداد ذرات موجود در عالم بیشتر است. با این حال، پیدا کردن پاسخ بهینه با تبدیل مسئله به یک مسئله برنامه ریزی خطی و حل آن با روش سیمپلکس تنها لحظه ای طول می کشد.
الگوریتم سیمپلکس که توسط جورج دانتزینگ شکل گرفت، مسائل برنامه ریزی خطی را به این ترتیب حل می کند که یک جواب قابل قبول در یکی از رئوس چندضلعی فراهم می کند و سپس در راستای اضلاع چندضلعی به طرف رئوسی با مقدار بالاتری از تابع هدف حرکت می کند تا این که به نقطه بهینه برسد. اگرچه در عمل این الگوریتم بسیار کارآمد است و می تواند با در نظر گرفتن برخی پیش گیری های مربوط به جلوگیری از ایجاد دور، با اطمینان جواب بهینه مطلق را بیابد، اما در حالاتی که به اصطلاح بدترین حالت نامیده می شوند عملکرد بدی دارد. تا حدی که می توان مسائل برنامه ریزی خطی طراحی کرد که روش سیمپلکس برای حلشان در برخی مراحل زمانی از مرتبه زمانی نمایی نیاز داشته باشد. حتی در دورانی دانشمندان نمی دانستند که این مسائل راه حل چندجمله ای هم دارند.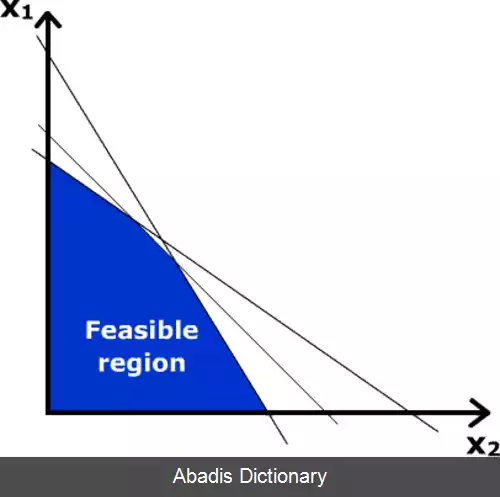

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمسئلهٔ حل مجموعه ای از نامعادلات خطی از زمان فوریه مطرح بوده است. برنامه ریزی خطی به عنوان یک مدل ریاضی در زمان جنگ جهانی دوم شکل گرفت تا خرج ها و بازگشت های مالی را طوری سامان بخشد که به کاهش هزینه های ارتش و افزایش خسارات دشمن بینجامد. این طرح تا سال ۱۹۴۷ سری باقی ماند. پس از جنگ، بسیاری از صنایع به استفاده از آن پرداختند. پایه گذاران این حوزه جورج دانتزیگ منتشرکنندهٔ روش سیمپلکس در سال ۱۹۴۷، جان فون نویمان مطرح کننده نظریه دوگانگی در همان سال، و لئونید کانتروویچ ریاضیدان روس که از تکنیک های مشابهی پیش از دانتزینگ استفاده کرد و نوبل سال ۱۹۵۷ را برد هستند. نخستین بار در سال ۱۹۷۹ لئونید خاچیان نشان داد که مسئله برنامه ریزی خطی در مرتبه زمانی چندجمله ای قابل حل است. اما پیشرفت اساسی تر زمانی حاصل شد که نراندرا کارمارکار یک روش نقطه داخلی جدید برای حل این مسائل معرفی کرد. مثال دانتزینگ برای منتصب کردن هفتاد نفر به هفتاد شغل متمایز کارآمدی برنامه ریزی خطی را به نمایش می گذارد. توان محاسباتی لازم برای آزمودن همهٔ جایگشتهای ممکن این مسئله بسیار بالاست. این تعداد از تعداد ذرات موجود در عالم بیشتر است. با این حال، پیدا کردن پاسخ بهینه با تبدیل مسئله به یک مسئله برنامه ریزی خطی و حل آن با روش سیمپلکس تنها لحظه ای طول می کشد.
الگوریتم سیمپلکس که توسط جورج دانتزینگ شکل گرفت، مسائل برنامه ریزی خطی را به این ترتیب حل می کند که یک جواب قابل قبول در یکی از رئوس چندضلعی فراهم می کند و سپس در راستای اضلاع چندضلعی به طرف رئوسی با مقدار بالاتری از تابع هدف حرکت می کند تا این که به نقطه بهینه برسد. اگرچه در عمل این الگوریتم بسیار کارآمد است و می تواند با در نظر گرفتن برخی پیش گیری های مربوط به جلوگیری از ایجاد دور، با اطمینان جواب بهینه مطلق را بیابد، اما در حالاتی که به اصطلاح بدترین حالت نامیده می شوند عملکرد بدی دارد. تا حدی که می توان مسائل برنامه ریزی خطی طراحی کرد که روش سیمپلکس برای حلشان در برخی مراحل زمانی از مرتبه زمانی نمایی نیاز داشته باشد. حتی در دورانی دانشمندان نمی دانستند که این مسائل راه حل چندجمله ای هم دارند.


wiki: برنامه ریزی خطی
