بردار پوینتینگ، نامِ برداری در فیزیک است. اندازهٔ این بردار، چگالیِ انرژیِ الکترومغناطیسی را نشان می دهد که از واحدِ سطح در واحدِ زمان عبور می کند و واحدِ آن وات بر مترِ مربع ( W/m2 ) است. این بردار، به نامِ کسی که آن را به دست آورد، فیزیک دان انگلیسی جان پوینتینگ، نام گذاری شده است. این بردار از طریقِ رابطهٔ زیر، با میدانِ الکتریکی و میدانِ مغناطیسی، پیوند می یابد:
که در آن:
• S {\displaystyle \mathbf {S} \ } نشان دهندهٔ بردارِ پوینتینگ است.
• E {\displaystyle \mathbf {E} \ } نشان دهندهٔ بردارِ میدانِ الکتریکی است.
• B {\displaystyle \mathbf {B} \ } نشان دهندهٔ بردارِ میدانِ مغناطیسی است.
چگالیِ انرژیِ الکتریکی و چگالیِ انرژیِ مغناطیسی که در یک سیستم ذخیره شده است، هر کدام به ترتیب از رابطه هایِ زیر به دست می آیند:
در نتیجه چگالیِ انرژیِ کلِ ذخیره شده در فضا، عبارت است از:
موجِ الکترومغناطیسی در خلاء با سرعتِ نور منتشر می شود که آن را با c نمایش می دهیم. در بازه یِ زمانیِ Δ t ، این موج به اندازهٔ c Δ t به جلو رفته است. اگر یک میدانِ پیوستهٔ الکترومغناطیسی را در نظر بگیریم که در یک بازهٔ زمانیِ معین به سطحی با مساحتِ A می تابد، آن گاه از هر واحدِ سطح، طولِ c Δ t از میدانِ الکترومغناطیسی عبور کرده است. اگر انرژی هر واحد از طولِ عبور کرده برابر با u که همان چگالیِ انرژی است باشد آن گاه انرژیِ کلِ عبور کرده در واحدِ سطح در یک بازهٔ زمانیِ برابر خواهد بود: u ( c Δ t ) با تقسیم کردنِ انرژیِ کلِ عبوری بر زمانی که این انرژی عبور کرده است، انرژیِ کلِ عبور کرده از واحدِ سطح، در واحدِ زمان، به دست می آید:
حال با توجه به اینکه c 2 = 1 μ 0 ε 0 به راحتی می توان نشان داد که : u m و u e با هم برابر هستند. به علاوه، از آن جایی که موجِ الکترومغناطیسی، موجی عرضی است، میدان هایِ الکتریکی و مغناطیسیِ آن برهم عمود هستند و می توان نشان داد که | E | = c | B | در نتیجه با جایگذاریِ این دو رابطه در رابطهٔ بالا، رابطهٔ نهایی برایِ اندازه یِ بردارِ پوینتینگ این گونه به دست می آید:
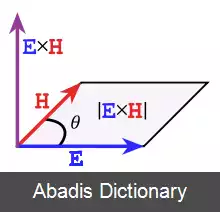
بردارِ پوینتینگ، که از تعمیمِ این رابطه به بردارها ساخته شده است، برداری است که جهتِ آن، جهتِ سطحِ عبوری را نشان می دهد - با توجه به عمود بودنِ میدانِ الکتریکی و مغناطیسی برهم و عرضی بودنِ موج. - و اندازهٔ آن، اندازهٔ انرژیِ عبوری از واحدِ سطح را در واحدِ زمان نشان می دهد. با توجه به آن که B = μ 0 H ، این بردار، آن طور که خودِ جان پوینتینگ، آن را نمایش می داد و به فرمِ آبراهام معروف است، خواهد بود: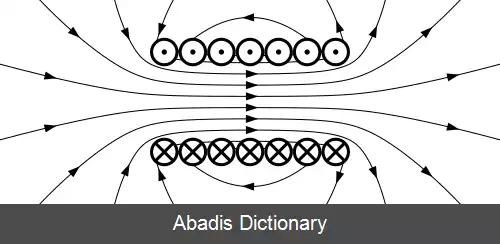
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفکه در آن:
• S {\displaystyle \mathbf {S} \ } نشان دهندهٔ بردارِ پوینتینگ است.
• E {\displaystyle \mathbf {E} \ } نشان دهندهٔ بردارِ میدانِ الکتریکی است.
• B {\displaystyle \mathbf {B} \ } نشان دهندهٔ بردارِ میدانِ مغناطیسی است.
چگالیِ انرژیِ الکتریکی و چگالیِ انرژیِ مغناطیسی که در یک سیستم ذخیره شده است، هر کدام به ترتیب از رابطه هایِ زیر به دست می آیند:
در نتیجه چگالیِ انرژیِ کلِ ذخیره شده در فضا، عبارت است از:
موجِ الکترومغناطیسی در خلاء با سرعتِ نور منتشر می شود که آن را با c نمایش می دهیم. در بازه یِ زمانیِ Δ t ، این موج به اندازهٔ c Δ t به جلو رفته است. اگر یک میدانِ پیوستهٔ الکترومغناطیسی را در نظر بگیریم که در یک بازهٔ زمانیِ معین به سطحی با مساحتِ A می تابد، آن گاه از هر واحدِ سطح، طولِ c Δ t از میدانِ الکترومغناطیسی عبور کرده است. اگر انرژی هر واحد از طولِ عبور کرده برابر با u که همان چگالیِ انرژی است باشد آن گاه انرژیِ کلِ عبور کرده در واحدِ سطح در یک بازهٔ زمانیِ برابر خواهد بود: u ( c Δ t ) با تقسیم کردنِ انرژیِ کلِ عبوری بر زمانی که این انرژی عبور کرده است، انرژیِ کلِ عبور کرده از واحدِ سطح، در واحدِ زمان، به دست می آید:
حال با توجه به اینکه c 2 = 1 μ 0 ε 0 به راحتی می توان نشان داد که : u m و u e با هم برابر هستند. به علاوه، از آن جایی که موجِ الکترومغناطیسی، موجی عرضی است، میدان هایِ الکتریکی و مغناطیسیِ آن برهم عمود هستند و می توان نشان داد که | E | = c | B | در نتیجه با جایگذاریِ این دو رابطه در رابطهٔ بالا، رابطهٔ نهایی برایِ اندازه یِ بردارِ پوینتینگ این گونه به دست می آید:
بردارِ پوینتینگ، که از تعمیمِ این رابطه به بردارها ساخته شده است، برداری است که جهتِ آن، جهتِ سطحِ عبوری را نشان می دهد - با توجه به عمود بودنِ میدانِ الکتریکی و مغناطیسی برهم و عرضی بودنِ موج. - و اندازهٔ آن، اندازهٔ انرژیِ عبوری از واحدِ سطح را در واحدِ زمان نشان می دهد. با توجه به آن که B = μ 0 H ، این بردار، آن طور که خودِ جان پوینتینگ، آن را نمایش می داد و به فرمِ آبراهام معروف است، خواهد بود:


wiki: بردار پوئینتینگ
