اساساً الگوریتم پیدا کردن ریشه یا ریشه یابی، یک الگوریتم برای پیدا کردن ریشه های توابع پیوسته است.
یک ریشه از تابع f هنگامی پیدا می شود که x در معادلهٔ f ( x ) = 0 صدق کند و به آن x ریشهٔ تابع f می گوییم یا در معادلهٔ زیر هنگامی ریشهٔ f را پیدا می کنیم که حاصل تفریق دو تابع دیگر برابر ۰ شود.
f ( x ) = g ( x ) − h ( x ) => g ( x ) − f ( x ) = 0 => g ( x ) = f ( x )
به طور کلی ریشه های بسیاری از توابع را نمی توان به صورت دقیق محاسبه کرد و الگوریتم پیدا کردن ریشه ( Root - finding algorithm ) به ما کمک می کند که به صورت تقریبی آنها را محاسبه کنیم.
اکثر الگوریتم های ریشه یابی با استفاده از انتخاب دنباله ای از اعداد امیدوارند که این دنباله به عنوان یک حد به سمت ریشه همگرایی داشته باشد. آنها با استفاده از یک یا چند حدس اولیه از ریشه، به عنوان مقادیر شروع می کنند سپس هر تکرار الگوریتم تقریب بهتری از ریشه را برای ما به ارمغان می آورد. [ ۱]
در این گونه روش ها با تعیین بازه های کوچک و استفاده از آنها در برخی فرمول ها سعی می کنیم که به ریشه دست پیدا کنیم. [ ۳]
این روش از ساده ترین و قابل اعتمادترین روش های تکراری برای حل معادلهٔ غیر خطی است. این روش همچنین به عنوان روش تقسیم باینری ( binary chopping ) یا نیمه بازه ( half - interval method ) نیز شناخته می شود.
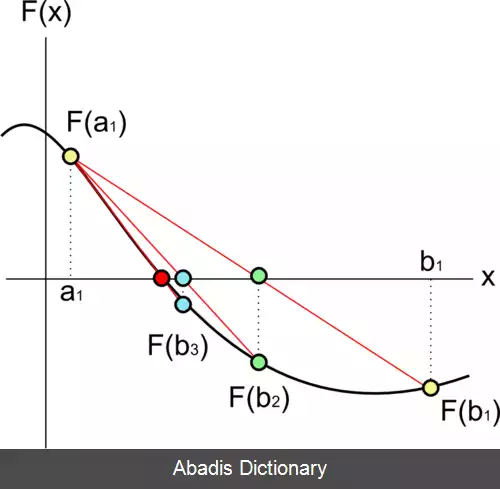
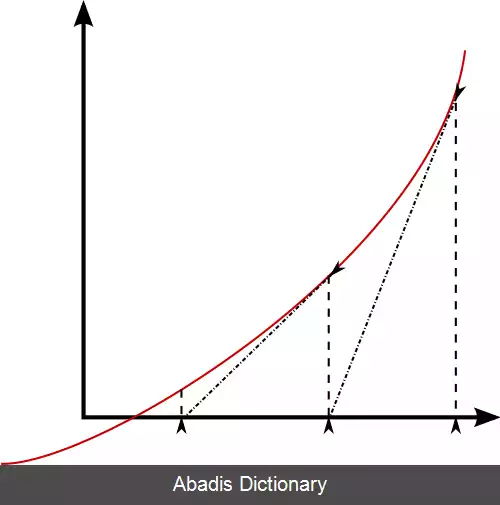
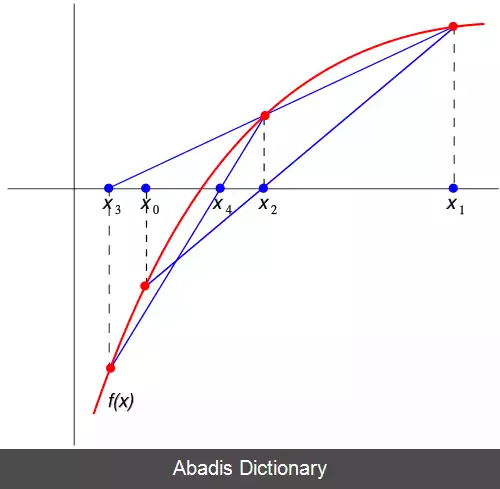
در این روش تابع f را به n بازهٔ مختلف تقسیم می کنیم تا ریشه ای مانند ϵ را پیدا کنیم بدین صورت که: i f ( f ( ( a n + b n ) 2 ) = 0 ) t h e n ϵ = ( a n + b n ) 2 i f ( f ( a n ) f ( ( a n + b n ) 2 ) < 0 ) t h e n s e t a n + 1 = a n ; b n + 1 = ( a n + b n ) 2 در غیر این صورت: s e t a n + 1 = a n + b n 2 ; b n + 1 = b n برای فهم بهتر به تصویر زیر توجه کنید: روش نابجایی در این روش مانند روش قبل تابع مورد نظر را بازه بازه می کنیم ولی در این روش سریع تر به این مسئله و رسیدن به ریشه اهمیت می دهیم. بدین صورت که: w = ( f ( b i − 1 ) a i − 1 − f ( a i − 1 ) b i − 1 ) f ( b i − 1 ) − f ( a i − 1 ) i f ( f ( a n ) f ( w ) ⩽ 0 ) t h e n s e t a n + 1 = a n ; b n + 1 = w در غیر این صورت a n + 1 = w ; b n + 1 = b n برای درک بهتر به تصویر زیر توجه کنید:regula falsi روش تعامل ( Interpolation ) [ ۴] بسیاری از روش های پیدا کردن ریشه از این روش استفاده می کنند. این روش شامل استفاده از آخرین مقادیر تقریبی محاسبات ریشه برای تقریب تابع توسط یک چندجمله ای از درجه پایین است که مقادیر مشابهی را در این ریشه های تقریبی می گیرد.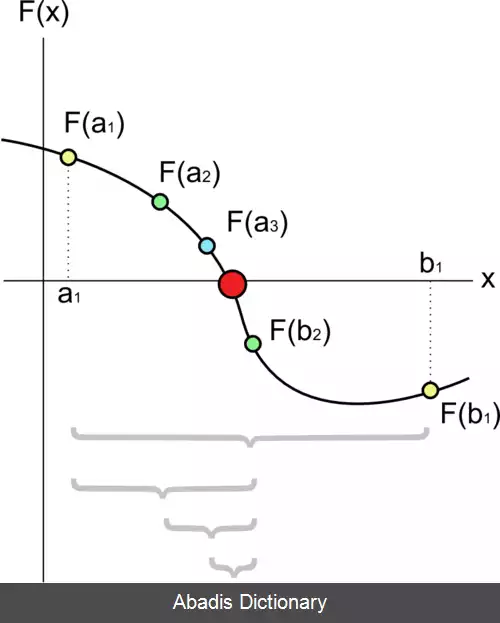
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک ریشه از تابع f هنگامی پیدا می شود که x در معادلهٔ f ( x ) = 0 صدق کند و به آن x ریشهٔ تابع f می گوییم یا در معادلهٔ زیر هنگامی ریشهٔ f را پیدا می کنیم که حاصل تفریق دو تابع دیگر برابر ۰ شود.
f ( x ) = g ( x ) − h ( x ) => g ( x ) − f ( x ) = 0 => g ( x ) = f ( x )
به طور کلی ریشه های بسیاری از توابع را نمی توان به صورت دقیق محاسبه کرد و الگوریتم پیدا کردن ریشه ( Root - finding algorithm ) به ما کمک می کند که به صورت تقریبی آنها را محاسبه کنیم.
اکثر الگوریتم های ریشه یابی با استفاده از انتخاب دنباله ای از اعداد امیدوارند که این دنباله به عنوان یک حد به سمت ریشه همگرایی داشته باشد. آنها با استفاده از یک یا چند حدس اولیه از ریشه، به عنوان مقادیر شروع می کنند سپس هر تکرار الگوریتم تقریب بهتری از ریشه را برای ما به ارمغان می آورد. [ ۱]
در این گونه روش ها با تعیین بازه های کوچک و استفاده از آنها در برخی فرمول ها سعی می کنیم که به ریشه دست پیدا کنیم. [ ۳]
این روش از ساده ترین و قابل اعتمادترین روش های تکراری برای حل معادلهٔ غیر خطی است. این روش همچنین به عنوان روش تقسیم باینری ( binary chopping ) یا نیمه بازه ( half - interval method ) نیز شناخته می شود.
در این روش تابع f را به n بازهٔ مختلف تقسیم می کنیم تا ریشه ای مانند ϵ را پیدا کنیم بدین صورت که: i f ( f ( ( a n + b n ) 2 ) = 0 ) t h e n ϵ = ( a n + b n ) 2 i f ( f ( a n ) f ( ( a n + b n ) 2 ) < 0 ) t h e n s e t a n + 1 = a n ; b n + 1 = ( a n + b n ) 2 در غیر این صورت: s e t a n + 1 = a n + b n 2 ; b n + 1 = b n برای فهم بهتر به تصویر زیر توجه کنید: روش نابجایی در این روش مانند روش قبل تابع مورد نظر را بازه بازه می کنیم ولی در این روش سریع تر به این مسئله و رسیدن به ریشه اهمیت می دهیم. بدین صورت که: w = ( f ( b i − 1 ) a i − 1 − f ( a i − 1 ) b i − 1 ) f ( b i − 1 ) − f ( a i − 1 ) i f ( f ( a n ) f ( w ) ⩽ 0 ) t h e n s e t a n + 1 = a n ; b n + 1 = w در غیر این صورت a n + 1 = w ; b n + 1 = b n برای درک بهتر به تصویر زیر توجه کنید:regula falsi روش تعامل ( Interpolation ) [ ۴] بسیاری از روش های پیدا کردن ریشه از این روش استفاده می کنند. این روش شامل استفاده از آخرین مقادیر تقریبی محاسبات ریشه برای تقریب تابع توسط یک چندجمله ای از درجه پایین است که مقادیر مشابهی را در این ریشه های تقریبی می گیرد.




