در نظریه گراف، الگوریتم دایکسترا ( به انگلیسی: Dijkstra's algorithm ) یکی از الگوریتم های پیمایش گراف است که توسط دانشمند هلندی علوم رایانه، اِدْسْخِر دیْکْسْترا در سال ۱۹۵۹ ارائه شد.
این الگوریتم یکی از الگوریتم های پیمایش گراف است که مسئلهٔ کوتاه ترین مسیر از مبدأ واحد را برای گراف های وزن داری که یال با وزن منفی ندارند، حل می کند و در نهایت با ایجاد درخت کوتاه ترین مسیر، کوتاه ترین مسیر از مبدأ به همهٔ رأس های گراف را به دست می دهد. همچنین می توان از این الگوریتم برای پیدا کردن کوتاه ترین مسیر از مبدأ تا رأس مقصد به این ترتیب بهره جست که در حین اجرای الگوریتم به محض پیداشدن کوتاه ترین مسیر از مبدأ به مقصد، الگوریتم را متوقف کرد.
الگوریتم دایکسترا یکی از الگوریتم های مورد استفاده برای محاسبه کوتاه ترین مسیر تک منبع ( single - source shortest path ) است و مشابه الگوریتم پریم می باشد در صورتی که گراف یال با وزن منفی داشته باشد، این الگوریتم درست کار نمی کند و می بایست از الگوریتم های دیگر نظیر الگوریتم بلمن - فورد که پیچیدگی زمانی آن ها بیشتر است استفاده کنیم.
خط مشی الگوریتم دایکسترا، مشابه با روش حریصانهٔ استفاده شده در الگوریتم پریم برای پیدا کردن زیر درخت فراگیر بهینه است.
نام این الگوریتم بر اساس نام ارائه دهنده هلندی آن، یعنی اِدسخِر دایکسترا انتخاب شده است. در منابع فارسی آن را به شکل های دِیکسترا، دکسترا، دایکسترا، دایجسترا، دیجسترا، دایجکسترا و دیجکسترا هم نوشته شده است، ولی جیمِ آن در تلفظ هلندی آن تلفظ نمی شود، لذا دو مورد اول صحیح هستند.
روند الگوریتم دایکسترا مطابق زیر می باشد:
۱ - انتخاب راس مبدا
۲ - مجموعهٔ S، شامل رئوس گراف، معین می شود. در شروع، این مجموعه تهی بوده و با پیشرفت الگوریتم، این مجموعه رئوسی که کوتاه ترین مسیر به آن ها یافت شده است را در بر می گیرد.
۳ - راس مبدأ با اندیس صفر را در داخل S قرار می دهد.
۴ - برای رئوس خارج از S، اندیسی معادل، طول یال + اندیس راس قبلی، در نظر می گیرد. اگر راس خارج از مجموعه دارای اندیس باشد، اندیس جدید کمترین مقدار از بین اندیس قبلی و طول یال + اندیس راس قبل، می باشد.
۵ - از رئوس خارج مجموعه، راسی با کمترین اندیس انتخاب شده و به مجموعهٔ S اضافه می گردد.
۶ - این کار را دوباره از مرحلهٔ ۴ ادامه داده تا راس مقصد وارد مجموعهٔ S شود.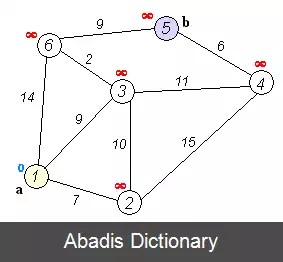

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاین الگوریتم یکی از الگوریتم های پیمایش گراف است که مسئلهٔ کوتاه ترین مسیر از مبدأ واحد را برای گراف های وزن داری که یال با وزن منفی ندارند، حل می کند و در نهایت با ایجاد درخت کوتاه ترین مسیر، کوتاه ترین مسیر از مبدأ به همهٔ رأس های گراف را به دست می دهد. همچنین می توان از این الگوریتم برای پیدا کردن کوتاه ترین مسیر از مبدأ تا رأس مقصد به این ترتیب بهره جست که در حین اجرای الگوریتم به محض پیداشدن کوتاه ترین مسیر از مبدأ به مقصد، الگوریتم را متوقف کرد.
الگوریتم دایکسترا یکی از الگوریتم های مورد استفاده برای محاسبه کوتاه ترین مسیر تک منبع ( single - source shortest path ) است و مشابه الگوریتم پریم می باشد در صورتی که گراف یال با وزن منفی داشته باشد، این الگوریتم درست کار نمی کند و می بایست از الگوریتم های دیگر نظیر الگوریتم بلمن - فورد که پیچیدگی زمانی آن ها بیشتر است استفاده کنیم.
خط مشی الگوریتم دایکسترا، مشابه با روش حریصانهٔ استفاده شده در الگوریتم پریم برای پیدا کردن زیر درخت فراگیر بهینه است.
نام این الگوریتم بر اساس نام ارائه دهنده هلندی آن، یعنی اِدسخِر دایکسترا انتخاب شده است. در منابع فارسی آن را به شکل های دِیکسترا، دکسترا، دایکسترا، دایجسترا، دیجسترا، دایجکسترا و دیجکسترا هم نوشته شده است، ولی جیمِ آن در تلفظ هلندی آن تلفظ نمی شود، لذا دو مورد اول صحیح هستند.
روند الگوریتم دایکسترا مطابق زیر می باشد:
۱ - انتخاب راس مبدا
۲ - مجموعهٔ S، شامل رئوس گراف، معین می شود. در شروع، این مجموعه تهی بوده و با پیشرفت الگوریتم، این مجموعه رئوسی که کوتاه ترین مسیر به آن ها یافت شده است را در بر می گیرد.
۳ - راس مبدأ با اندیس صفر را در داخل S قرار می دهد.
۴ - برای رئوس خارج از S، اندیسی معادل، طول یال + اندیس راس قبلی، در نظر می گیرد. اگر راس خارج از مجموعه دارای اندیس باشد، اندیس جدید کمترین مقدار از بین اندیس قبلی و طول یال + اندیس راس قبل، می باشد.
۵ - از رئوس خارج مجموعه، راسی با کمترین اندیس انتخاب شده و به مجموعهٔ S اضافه می گردد.
۶ - این کار را دوباره از مرحلهٔ ۴ ادامه داده تا راس مقصد وارد مجموعهٔ S شود.


wiki: الگوریتم دایکسترا
