در نظریهٔ گراف، جستجوی عمق اول ( به انگلیسی: Depth - first Search، به اختصار DFS ) یک الگوریتم پیمایش گراف است که برای پیمایش یا جستجوی یک گراف به کار می رود. روش جستجوی عمق اول برای پیمایش گراف، همان طور که از نامش پیداست «جستجوی رأس های عمیق تر در گراف تا زمانی که امکان دارد» است.
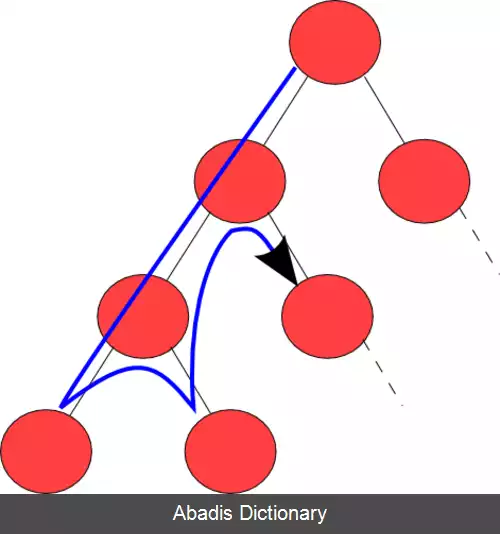
الگوریتم از یک راس دلخواه ( ریشه در درخت های ریشه دار ) شروع می کند و در هر مرحله همسایه های رأس جاری را از طریق یال های خروجی رأس جاری به ترتیب بررسی کرده و به محض روبه رو شدن با همسایه ای که قبلاً دیده نشده باشد، به صورت بازگشتی برای آن رأس به عنوان رأس جاری اجرا می شود. در صورتی که همهٔ همسایه ها قبلاً دیده شده باشند، الگوریتم عقب گرد می کند و اجرای الگوریتم برای رأسی که از آن به رأس جاری رسیده ایم، ادامه می یابد. به عبارتی الگوریتم تا آنجا که ممکن است، به عمق بیشتر می رود و در مواجهه با بن بست عقب گرد می کند. این فرایند تا زمانی که همهٔ رأس های قابل دستیابی از ریشه دیده شوند ادامه می یابد.
همچنین در مسائلی که حالات مختلف متناظر با رئوس یک گراف اند و حل مسئله مستلزم یافتن رأس هدف با خصوصیات مشخصی است، جستجوی عمق اول مفید است. در هر گام، الگوریتم در صورت امکان به اولین همسایهٔ دیده نشده یک رأس در گراف جستجو می رود تا به رأسی برسد که همهٔ همسایگانش دیده شده اند که در حالت اخیر، الگوریتم به اولین رأسی بر می گردد که همسایهٔ داشته باشد که هنوز دیده نشده باشد. این روند تا جایی ادامه می یابد که رأس هدف پیدا شود یا همهٔ مولفهٔ همبندی گراف پیمایش شود. البته پیاده سازی هوشمندانهٔ الگوریتم با انتخاب ترتیب مناسب برای بررسی همسایه های دیده نشدهٔ رأس جاری به صورتی که ابتدا الگوریتم به بررسی همسایه ای بپردازد که به صورت موضعی و با انتخابی حریصانه به رأس هدف نزدیک تر است، امکان پذیر خواهد بود که در کاهش زمان اجرا مؤثر است.
برای اجرای الگوریتم، از یک پشته استفاده می شود. بدین ترتیب که هر بار با ورود به یک رأس دیده نشده، آن رأس را در پشته قرار می دهیم و هنگام عقب گرد رأس را از پشته حذف می کنیم؛ بنابراین در تمام طول الگوریتم اولین عنصر پشته رأس در حال بررسی است.
وقتی در گراف های بزرگی جستجو می کنیم که امکان ذخیرهٔ کامل آن ها به علت محدودیت حافظه وجود ندارد، در صورتی که طول مسیر پیمایش شده توسط الگوریتم که از ریشه شروع شده، خیلی بزرگ شود، الگوریتم با مشکل مواجه خواهد شد. در واقع این راه حل ساده که «رئوسی را که تا به حال دیده ایم ذخیره کنیم» همیشه کار نمی کند. چرا که ممکن است حافظهٔ کافی نداشته باشیم. البته این مشکل با محدود کردن عمق جستجو در هر بار اجرای الگوریتم حل می شود که در نهایت به الگوریتم جستجوی عمق اول عمیق کننده تکراری خواهد انجامید.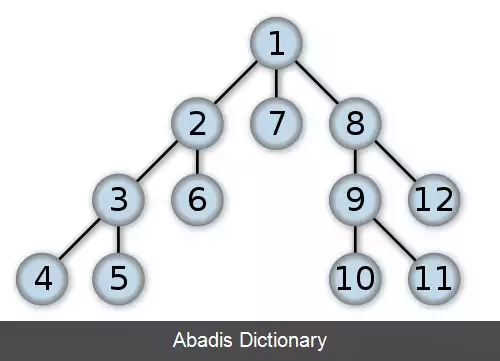
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفالگوریتم از یک راس دلخواه ( ریشه در درخت های ریشه دار ) شروع می کند و در هر مرحله همسایه های رأس جاری را از طریق یال های خروجی رأس جاری به ترتیب بررسی کرده و به محض روبه رو شدن با همسایه ای که قبلاً دیده نشده باشد، به صورت بازگشتی برای آن رأس به عنوان رأس جاری اجرا می شود. در صورتی که همهٔ همسایه ها قبلاً دیده شده باشند، الگوریتم عقب گرد می کند و اجرای الگوریتم برای رأسی که از آن به رأس جاری رسیده ایم، ادامه می یابد. به عبارتی الگوریتم تا آنجا که ممکن است، به عمق بیشتر می رود و در مواجهه با بن بست عقب گرد می کند. این فرایند تا زمانی که همهٔ رأس های قابل دستیابی از ریشه دیده شوند ادامه می یابد.
همچنین در مسائلی که حالات مختلف متناظر با رئوس یک گراف اند و حل مسئله مستلزم یافتن رأس هدف با خصوصیات مشخصی است، جستجوی عمق اول مفید است. در هر گام، الگوریتم در صورت امکان به اولین همسایهٔ دیده نشده یک رأس در گراف جستجو می رود تا به رأسی برسد که همهٔ همسایگانش دیده شده اند که در حالت اخیر، الگوریتم به اولین رأسی بر می گردد که همسایهٔ داشته باشد که هنوز دیده نشده باشد. این روند تا جایی ادامه می یابد که رأس هدف پیدا شود یا همهٔ مولفهٔ همبندی گراف پیمایش شود. البته پیاده سازی هوشمندانهٔ الگوریتم با انتخاب ترتیب مناسب برای بررسی همسایه های دیده نشدهٔ رأس جاری به صورتی که ابتدا الگوریتم به بررسی همسایه ای بپردازد که به صورت موضعی و با انتخابی حریصانه به رأس هدف نزدیک تر است، امکان پذیر خواهد بود که در کاهش زمان اجرا مؤثر است.
برای اجرای الگوریتم، از یک پشته استفاده می شود. بدین ترتیب که هر بار با ورود به یک رأس دیده نشده، آن رأس را در پشته قرار می دهیم و هنگام عقب گرد رأس را از پشته حذف می کنیم؛ بنابراین در تمام طول الگوریتم اولین عنصر پشته رأس در حال بررسی است.
وقتی در گراف های بزرگی جستجو می کنیم که امکان ذخیرهٔ کامل آن ها به علت محدودیت حافظه وجود ندارد، در صورتی که طول مسیر پیمایش شده توسط الگوریتم که از ریشه شروع شده، خیلی بزرگ شود، الگوریتم با مشکل مواجه خواهد شد. در واقع این راه حل ساده که «رئوسی را که تا به حال دیده ایم ذخیره کنیم» همیشه کار نمی کند. چرا که ممکن است حافظهٔ کافی نداشته باشیم. البته این مشکل با محدود کردن عمق جستجو در هر بار اجرای الگوریتم حل می شود که در نهایت به الگوریتم جستجوی عمق اول عمیق کننده تکراری خواهد انجامید.



wiki: الگوریتم جستجوی عمق اول
