در نظریهٔ گراف، جستجوی سطح - اول ( به انگلیسی: Breadth - first Search، به اختصار: BFS ) یکی از الگوریتم های پیمایش گراف است.
استراتژی جستجوی سطح اول برای پیمایش گراف، همان طور که از نامش پیداست «جستجوی سطح به سطح گراف» است.
الگوریتم از ریشه شروع می کند ( در گراف ها یا درخت های بدون ریشه رأس دلخواهی به عنوان ریشه انتخاب می شود ) و آن را در سطح یک قرار می دهد. سپس در هر مرحله همهٔ همسایه های رئوس آخرین سطح دیده شده را که تا به حال دیده نشده اند بازدید می کند و آنها را در سطح بعدی می گذارد. این فرایند زمانی متوقف می شود که همهٔ همسایه های رئوس آخرین سطح قبلاً دیده شده باشند. همچنین در مسائلی که حالات مختلف متناظر با رئوس یک گراف اند و حل مسئله مستلزم یافتن رأس هدف با خصوصیات مشخصی است که در عین حال در بین همهٔ رئوس هدف با آن خصوصیات به ریشه نزدیک ترین باشد، جستجوی سطح اول به صورت غیرخلاق عمل می کند. بدین ترتیب که الگوریتم هر دفعه همهٔ همسایه های یک رأس را بازدید کرده و سپس به سراغ رأس بعدی می رود و بنابراین گراف سطح به سطح پیمایش خواهد شد. این روند تا جایی ادامه می یابد که رأس هدف پیدا شود یا احتمالاً همهٔ گراف پیمایش شود. براساس آنچه گفته شد پیاده سازی هوشمندانهٔ الگوریتم آنقدر مؤثر نخواهد بود.
از دیدگاه عملی، برای پیاده سازی این الگوریتم از صف استفاده می شود. بدین ترتیب که در ابتدا ریشه در صف قرار می گیرد. سپس هر دفعه عنصر ابتدای صف بیرون کشیده شده، همسایگانش بررسی شده و هر همسایه ای که تا به حال دیده نشده باشد به انتهای صف اضافه می شود. جزئیات پیاده سازی در ادامه خواهد آمد.
پیاده سازی این الگوریتم مشابه پیاده سازی جستجوی عمق اول است با این تفاوت که به جای پشته از صف استفاده می شود. در این جا نیز مانند جستجوی عمق اول، preWORK را برای انعطاف بیشتر الگوریتم در نظر می گیریم که در زمان بررسی کردن هر رأس خارج شده از صف انجام می شود.
الگوریتم جستجوی اول سطح به صورت زیر است. آرایه Visited برای تعیین رئوس ملاقات شده بکار می رود. از یک صف برای نگهداشتن رئوس مجاور استفاده می شود. هر بار که راسی ملاقات می شود کلیه رئوس مجاور آن در صف اضافه می شود. پیمایش از راسی که از صف برداشته می شود ادامه پیدا می کند.
الگوریتم:
• یکی به انتهای صف در گره جدید اضافه کن
• در آن صف به جلو حرکت کرده و گره بعدی را امتحان کن الف - اگر پاسخ مورد نظر در آن گره پیدا شد، اتمام جستجو و نتیجه را برگردان ب - در غیر اینصورت زیرمجموعه های ( فرزندان ) مستقیم گره هایی را که جستجونشده بررسی کن
• اگر صف دیگری وجود نداشت و همه گره ها بررسی شد، اتمام جستجو و «چیزی پیدا نشد» را برگردان
• اگر صف به پایان نرسید برو مرحله ۲.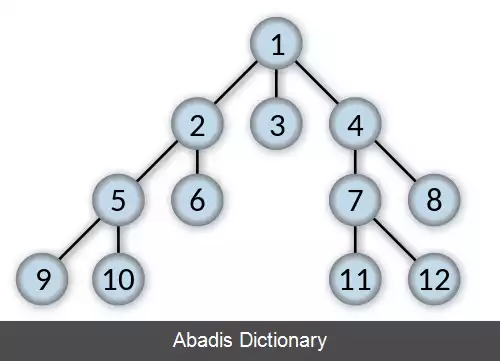
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاستراتژی جستجوی سطح اول برای پیمایش گراف، همان طور که از نامش پیداست «جستجوی سطح به سطح گراف» است.
الگوریتم از ریشه شروع می کند ( در گراف ها یا درخت های بدون ریشه رأس دلخواهی به عنوان ریشه انتخاب می شود ) و آن را در سطح یک قرار می دهد. سپس در هر مرحله همهٔ همسایه های رئوس آخرین سطح دیده شده را که تا به حال دیده نشده اند بازدید می کند و آنها را در سطح بعدی می گذارد. این فرایند زمانی متوقف می شود که همهٔ همسایه های رئوس آخرین سطح قبلاً دیده شده باشند. همچنین در مسائلی که حالات مختلف متناظر با رئوس یک گراف اند و حل مسئله مستلزم یافتن رأس هدف با خصوصیات مشخصی است که در عین حال در بین همهٔ رئوس هدف با آن خصوصیات به ریشه نزدیک ترین باشد، جستجوی سطح اول به صورت غیرخلاق عمل می کند. بدین ترتیب که الگوریتم هر دفعه همهٔ همسایه های یک رأس را بازدید کرده و سپس به سراغ رأس بعدی می رود و بنابراین گراف سطح به سطح پیمایش خواهد شد. این روند تا جایی ادامه می یابد که رأس هدف پیدا شود یا احتمالاً همهٔ گراف پیمایش شود. براساس آنچه گفته شد پیاده سازی هوشمندانهٔ الگوریتم آنقدر مؤثر نخواهد بود.
از دیدگاه عملی، برای پیاده سازی این الگوریتم از صف استفاده می شود. بدین ترتیب که در ابتدا ریشه در صف قرار می گیرد. سپس هر دفعه عنصر ابتدای صف بیرون کشیده شده، همسایگانش بررسی شده و هر همسایه ای که تا به حال دیده نشده باشد به انتهای صف اضافه می شود. جزئیات پیاده سازی در ادامه خواهد آمد.
پیاده سازی این الگوریتم مشابه پیاده سازی جستجوی عمق اول است با این تفاوت که به جای پشته از صف استفاده می شود. در این جا نیز مانند جستجوی عمق اول، preWORK را برای انعطاف بیشتر الگوریتم در نظر می گیریم که در زمان بررسی کردن هر رأس خارج شده از صف انجام می شود.
الگوریتم جستجوی اول سطح به صورت زیر است. آرایه Visited برای تعیین رئوس ملاقات شده بکار می رود. از یک صف برای نگهداشتن رئوس مجاور استفاده می شود. هر بار که راسی ملاقات می شود کلیه رئوس مجاور آن در صف اضافه می شود. پیمایش از راسی که از صف برداشته می شود ادامه پیدا می کند.
الگوریتم:
• یکی به انتهای صف در گره جدید اضافه کن
• در آن صف به جلو حرکت کرده و گره بعدی را امتحان کن الف - اگر پاسخ مورد نظر در آن گره پیدا شد، اتمام جستجو و نتیجه را برگردان ب - در غیر اینصورت زیرمجموعه های ( فرزندان ) مستقیم گره هایی را که جستجونشده بررسی کن
• اگر صف دیگری وجود نداشت و همه گره ها بررسی شد، اتمام جستجو و «چیزی پیدا نشد» را برگردان
• اگر صف به پایان نرسید برو مرحله ۲.

wiki: الگوریتم جستجوی سطح اول
