الگوریتم ارسال - برچسب ( به انگلیسی: push–relabel algorithm ) یکی از کارآمدترین الگوریتم ها برای محاسبهٔ یک مسئله بیشینه جریان است. الگوریتم عمومی دارای پیچیدگی زمانی O ( V 2 E ) است، در حالی که پیاده سازی آن با قانون شیوهٔ رأس ها به صورت FIFO دارای زمان اجرای O ( V 3 ) ، با شیوهٔ انتخاب فعال ترین رأس دارای پیچیدگی زمانی O ( V 2 E ) و با پیاده سازی با کمک داده ساختار درخت پویای ترجان و اسلیتور دارای زمان اجرای O ( V E log ( V 2 / E ) ) است. مجانباً این الگوریتم، از الگوریتم ادموند - کارپ که زمان اجرای آن O ( V E 2 ) است کاراتر است.
شبکه جریان O ( V E 2 ) داده شده که دارای ظرفیت ( به انگلیسی: capacity ) از گره u تا گره v است که به صورت c ( u , v ) داده شده، دارای منبع ( به انگلیسی: s ( source و چاهک ( به انگلیسی: t ( sink است. می خواهیم بیشترین میزان جریان را که می شود درون شبکه از s به t فرستاد را بیابیم. دو نوع عملیات روی گره ها انجام می شود: push و relabel. به طور کلی داریم:
• f ( u , v ) {\displaystyle f ( u, v ) } . جریان از u به v. ظرفیت قابل استفاده برابر است با c ( u , v ) − f ( u , v ) {\displaystyle c ( u, v ) - f ( u, v ) } .
• h e i g h t ( u ) {\displaystyle height ( u ) } . تنها در صورتی از u به v عمل push را انجام می دهیم که h e i g h t ( u ) > h e i g h t ( v ) {\displaystyle height ( u ) > height ( v ) } . به ازای همهٔ مقادیر u مقدار h e i g h t ( u ) {\displaystyle height ( u ) } یک عدد صحیح غیر منفی است.
• e x c e s s ( u ) {\displaystyle excess ( u ) } . حاصل جمع جریان وارد شده و خارج شده از u.
بعد از هر گام الگوریتم، جریان یک پیش جریان ( به انگلیسی: preflow ) است که شرایط زیر را دارد:
• f ( u , v ) ≤ c ( u , v ) {\displaystyle \ f ( u, v ) \leq c ( u, v ) } . جریان بین u {\displaystyle u} و v {\displaystyle v} از ظرفیت بیشتر نباشد.
• f ( u , v ) = − f ( v , u ) {\displaystyle \ f ( u, v ) = - f ( v, u ) } . جریان شبکه را در هر دو جهت حفظ می کنیم.
• به ازای تمام گره ها به صورت u ≠ s {\displaystyle u\neq s} ، ∑ v f ( v , u ) = e x c e s s ( u ) ≥ 0 {\displaystyle \ \sum _{v}f ( v, u ) =excess ( u ) \geq 0} . تنها منبع امکان ایجاد جریان داشته باشد.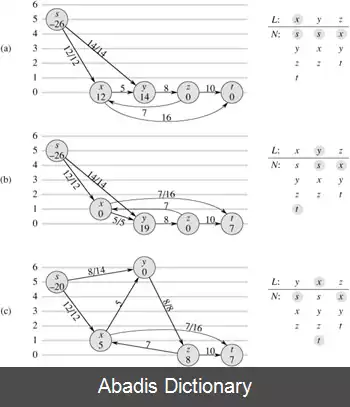

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفشبکه جریان O ( V E 2 ) داده شده که دارای ظرفیت ( به انگلیسی: capacity ) از گره u تا گره v است که به صورت c ( u , v ) داده شده، دارای منبع ( به انگلیسی: s ( source و چاهک ( به انگلیسی: t ( sink است. می خواهیم بیشترین میزان جریان را که می شود درون شبکه از s به t فرستاد را بیابیم. دو نوع عملیات روی گره ها انجام می شود: push و relabel. به طور کلی داریم:
• f ( u , v ) {\displaystyle f ( u, v ) } . جریان از u به v. ظرفیت قابل استفاده برابر است با c ( u , v ) − f ( u , v ) {\displaystyle c ( u, v ) - f ( u, v ) } .
• h e i g h t ( u ) {\displaystyle height ( u ) } . تنها در صورتی از u به v عمل push را انجام می دهیم که h e i g h t ( u ) > h e i g h t ( v ) {\displaystyle height ( u ) > height ( v ) } . به ازای همهٔ مقادیر u مقدار h e i g h t ( u ) {\displaystyle height ( u ) } یک عدد صحیح غیر منفی است.
• e x c e s s ( u ) {\displaystyle excess ( u ) } . حاصل جمع جریان وارد شده و خارج شده از u.
بعد از هر گام الگوریتم، جریان یک پیش جریان ( به انگلیسی: preflow ) است که شرایط زیر را دارد:
• f ( u , v ) ≤ c ( u , v ) {\displaystyle \ f ( u, v ) \leq c ( u, v ) } . جریان بین u {\displaystyle u} و v {\displaystyle v} از ظرفیت بیشتر نباشد.
• f ( u , v ) = − f ( v , u ) {\displaystyle \ f ( u, v ) = - f ( v, u ) } . جریان شبکه را در هر دو جهت حفظ می کنیم.
• به ازای تمام گره ها به صورت u ≠ s {\displaystyle u\neq s} ، ∑ v f ( v , u ) = e x c e s s ( u ) ≥ 0 {\displaystyle \ \sum _{v}f ( v, u ) =excess ( u ) \geq 0} . تنها منبع امکان ایجاد جریان داشته باشد.



wiki: الگوریتم ارسال برچسب
