افراز عدد صحیح

در این مقاله از افرازهای یک عدد صحیح یا از آنچه که با گردایه ای از اشیاء یکسان هم ارز است بحث می کنیم. در حالتی که اشیاء یکسان نباشند، مسئله تحت عنوان «افرازهای یک مجموعه» در می آید که در بحث این مقال نیست.
چون تعداد افرازهای ۵ برابر ۷ است، می نویسیم p ( 5 ) = 7 ؛ به طور کلی فرض کنیم p ( n ) تعداد افرازهای عدد صحیح مثبت n را نشان دهد. در افرازی مانند ۲ + ۳ بالا هریک از اعداد ۳ و ۲ را یک جمع وند می گویند؛ بنابراین عدد ۵ دارای افراز با یک جمع وند، دو افراز با دو جمع وند، دو افراز با سه جمع وند، یک افراز با چهار جمع وند و یک افراز با پنج جمع وند است. در حالی که ۵ دارای دو افراز با سه جمع وند است، معادله x 1 + x 2 + x 3 = 5 در مجموعه اعداد صحیح مثبت دارای شش جواب است که عبارت اند از:
( ۱٬۳٬۱ ) ( ۳٬۱٬۱ ) ( ۱٬۱٬۳ ) ( ۲٬۲٬۱ ) ( ۲٬۱٬۲ ) ( ۱٬۲٬۲ )
در شمردن تعداد جواب های یک معادله، ترتیب در نظر گرفته می شود؛ ولی در شمردن تعداد افرازها، ترتیب جمع وندها مفهومی ندارد.
به افرازهای ۶ توجه کنید:
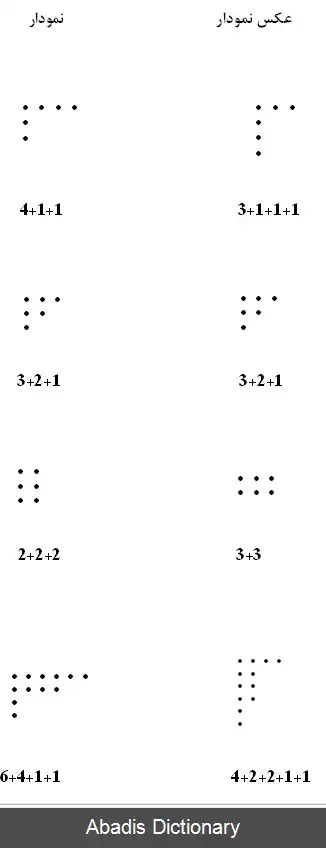
۳+۳ , ۵+۱ , ۴+۲ ۲+۲+۲ , ۳+۲+۱ , ۴+۱+۱{{سخ} , ۲+۲+۱+۱ , ۲+۱+۱+۱+۱ , ۱+۱+۱+۱+۱+۱ فهرست ۲ '
یازده افراز وجود دارد، بنابراین می نویسیم p ( 6 ) =۱۰. همچنین می بینیم که تعداد افرازهای ۶
است.
تعداد افرازهایn را که تعداد جمع وندهای آنها کوچکتر یا مساویk است با نماد q k ( n ) نشان خواهیم داد. به ازای n=۶، فهرست ( ۲ ) ی بالا نشان می دهد که:
q 6 ( 6 ) = 11 ∗ ∗ ∗ q 5 ( 6 ) = 10 ∗ ∗ ∗ q 4 ( 6 ) = 9 ∗ ∗ ∗ q 3 ( 6 ) = 7 ∗ ∗ ∗ q 2 ( 6 ) = 4 ∗ ∗ ∗ q 1 ( 6 ) = 1
چون عدد ۶ نمی تواند به بیشتر از شش جمع وند افراز شود، انتظار داریم که q 6 ( 6 ) همان q ( 6 ) باشد. به همین ترتیب، به معنای تعداد افرازهایn است که دارای n جمع وند یا کمتراز n جمع وند است و بنابراین
همچنین می توان افرازها را بر حسب اندازه جمع وندها رده بندی کرد. فهرست ( ۱ ) نشان می دهد که تعداد افرازهای ۶،
به شباهت این فهرست با فهرست ( ۲ ) توجه کنید. همان طوری که خواهیم دید این امر تصادفی نیست. به علاوه اگر q k ( n ) را تعداد افرازهایی ازn تعریف کنیم که هیچ یک از جمع وندهای آن ازk بزرگتر نباشد، نتیجه می گیریم که:
p 6 ( 6 ) = 11   p 5 ( 6 ) = 10   p 4 ( 6 ) = 9   p 3 ( 6 ) = 7   p 2 ( 6 ) = 4   p 1 ( 6 ) = 1