در هندسه، اصل پلی فیر ( به انگلیسی: Playfair's Axiom ) ، اصلی است که می توان از آن به جای اصل پنجم اقلیدس بهره جست ( اصل توازی اقلیدس ) :
در یک صفحه، برای خط دلخواه و نقطه دلخواهی که روی آن قرار نداشته باشد، حداکثر یک خط موازی با خط مذکور وجود دارد که از آن نقطه عبور کند. [ ۱]
این اصل با اصل توازی اقلیدس، در بستر هندسه اقلیدسی معادل بوده[ ۲] و به نام ریاضیدان اسکاتلندی، جان پلی فیر نامگذاری شده است. کلمه «حداکثر» در تعریف، همه آن چیزی که نیاز است را می دهد، چرا که می توان آن را از باقیمانده اصولی که می گویند حداقل یک خط موازی وجود دارد، بدست آورد. این گزاره را اغلب با این عبارت می نویسند: «یک و تنها یک خط موازی وجود دارد». در کتاب اصول اقلیدس، دو خط را موازی گویند اگر هیچگاه همدیگر را قطع نکرده و از سایر خصوصیات خطوط موازی نیز استفاده نشده باشد. [ ۳] [ ۴]
این اصل نه تنها در هندسه اقلیدسی، بلکه در مطالعه گسترده تر، شامل هندسه آفینی نیز به کار رفته است. در هندسه آفینی، مفهوم توازی نقش مرکزی را بازی می کند. در بستر هندسه آفین، شکل قوی تری از اصل پلی فیر وجود دارد ( که در آن کلمه «حداکثر» با «یک و تنها یک» جانشین شده است ) ، چرا که اصول موضوعه های هندسه خنثی، جهت ارائه اثبات وجود خط موازی موجود نیستند. نسخه پلی فیر از این اصل چنان معروف شده که اغلب به آن اصل توازی اقلیدس گفته می شود، [ ۵] گرچه که نسخه اقلیدس از این اصل، متفاوت می باشد. نتیجه ای از این اصل، این است که رابطه دوتایی موازی بودن خطوط، یک رابطه سری می باشد.
↑ ( Playfair 1846، ص. 29 ) ↑ به بیان دقیق تر، در بستر هندسه مطلق ↑ Euclid's elements, Book I, definition 23 ↑ ( Heath 1956، Vol. 1, p. 190 ) ↑ به عنوان مثال، رافائل آرتزی ( 1965 ) ، هندسه خطی، صفحه 202، انتشارات ادیسون - وسلی
• مشارکت کنندگان ویکی پدیا. «Playfair's Axiom». در دانشنامهٔ ویکی پدیای انگلیسی، بازبینی شده در ۳۰ مهٔ ۲۰۲۱.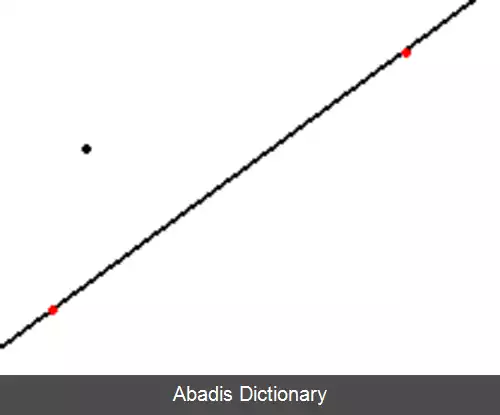
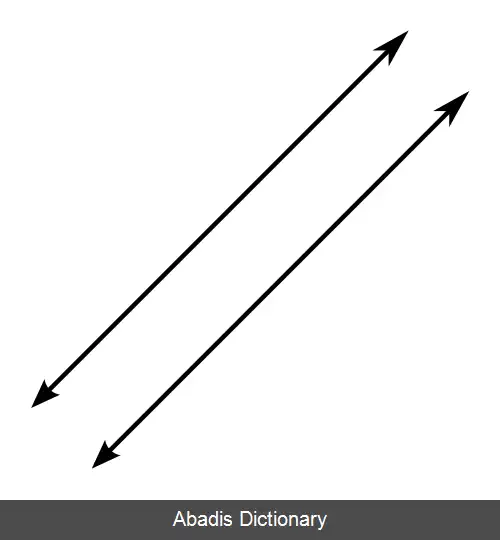
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر یک صفحه، برای خط دلخواه و نقطه دلخواهی که روی آن قرار نداشته باشد، حداکثر یک خط موازی با خط مذکور وجود دارد که از آن نقطه عبور کند. [ ۱]
این اصل با اصل توازی اقلیدس، در بستر هندسه اقلیدسی معادل بوده[ ۲] و به نام ریاضیدان اسکاتلندی، جان پلی فیر نامگذاری شده است. کلمه «حداکثر» در تعریف، همه آن چیزی که نیاز است را می دهد، چرا که می توان آن را از باقیمانده اصولی که می گویند حداقل یک خط موازی وجود دارد، بدست آورد. این گزاره را اغلب با این عبارت می نویسند: «یک و تنها یک خط موازی وجود دارد». در کتاب اصول اقلیدس، دو خط را موازی گویند اگر هیچگاه همدیگر را قطع نکرده و از سایر خصوصیات خطوط موازی نیز استفاده نشده باشد. [ ۳] [ ۴]
این اصل نه تنها در هندسه اقلیدسی، بلکه در مطالعه گسترده تر، شامل هندسه آفینی نیز به کار رفته است. در هندسه آفینی، مفهوم توازی نقش مرکزی را بازی می کند. در بستر هندسه آفین، شکل قوی تری از اصل پلی فیر وجود دارد ( که در آن کلمه «حداکثر» با «یک و تنها یک» جانشین شده است ) ، چرا که اصول موضوعه های هندسه خنثی، جهت ارائه اثبات وجود خط موازی موجود نیستند. نسخه پلی فیر از این اصل چنان معروف شده که اغلب به آن اصل توازی اقلیدس گفته می شود، [ ۵] گرچه که نسخه اقلیدس از این اصل، متفاوت می باشد. نتیجه ای از این اصل، این است که رابطه دوتایی موازی بودن خطوط، یک رابطه سری می باشد.
↑ ( Playfair 1846، ص. 29 ) ↑ به بیان دقیق تر، در بستر هندسه مطلق ↑ Euclid's elements, Book I, definition 23 ↑ ( Heath 1956، Vol. 1, p. 190 ) ↑ به عنوان مثال، رافائل آرتزی ( 1965 ) ، هندسه خطی، صفحه 202، انتشارات ادیسون - وسلی
• مشارکت کنندگان ویکی پدیا. «Playfair's Axiom». در دانشنامهٔ ویکی پدیای انگلیسی، بازبینی شده در ۳۰ مهٔ ۲۰۲۱.


wiki: اصل پلی فیر
