در ترکیبیات اصل شمول و عدم شمول یک تکنیک شمارش است که روش معمول شمارش اعضای اجتماع دو مجموعه متناهی - که به صورت زیر است - را بسط می دهد.
که A و B دو مجموعهٔ متناهی اند و |S| نمایانگر تعداد اعضای مجموعهٔ متناهی S است. این فرمول بیان می کند که مجموع اندازهٔ دو مجموعه ممکن است بزرگتر از اندازهٔ اجتماع آن ها باشد چون بعضی از اعضا شاید دو بار شمرده شوند. اعضایی که دو بار شمرده شده اند همان اعضایی اند که در اشتراک دو مجموعه حضور دارند بنابراین با کم کردن این تعداد، اندازهٔ واقعی مجموعهٔ اجتماع بدست می آید. این اصل در حالتی که سه مجموعه داریم واضح تر دیده می شود:
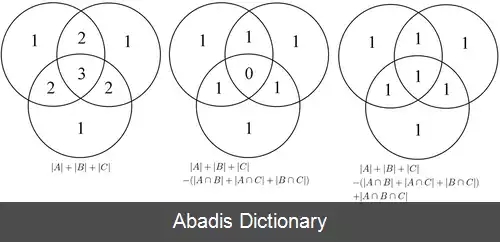
این فرمول می تواند به این صورت امتحان شود که بشماریم هر ناحیه در نمودار ون چند بار در سمت راست فرمول شمرده شده است.
بسط نتایج این مثال ها اصل شمول و عدم شمول را بدست می دهد: برای یافتن اندازهٔ اجتماع n مجموعه،
• اندازهٔ هر مجموعه را اضافه کنید،
• اندازهٔ اشتراک دو به دو مجموعه ها را کم کنید،
• اندازهٔ اشتراک هر سه تایی از مجموعه ها را اضافه کنید،
• اندازهٔ اشتراک هر چهارتایی از مجموعه ها را کم کنید،
• اندازهٔ اشتراک هر پنج تایی از مجموعه ها را اضافه کنید،
• به همین صورت ادامه دهید تا زمانی که اندازهٔ اشتراک nتایی مجموعه ها اضافه ( برای n فرد ) یا کم ( برای n زوج ) شود.
این اسم از اینجا آمده که این اصل براساس یک سری شمول و عدم شمول استوار است. این مفهوم به ابراهام دو مواور ( ۱۷۱۸ ) نسبت داده می شود، ولی بار اول در مقاله ای از دنیل داسیلوا ( ۱۸۵۴ ) و بعداً در مقاله ای از جیمز جوزف سیلوستر ( ۱۸۸۳ ) ظاهر شد. به همین دلیل گاهی این اصل به عنوان فرمول داسیلوا یا سیلوستر شناخته می شود.
از آنجایی که احتمالات متناهی براساس اندازهٔ فضای احتمال محاسبه می شوند، زمانی که اندازهٔ مجموعه ها با احتمالات متناهی جایگزین می شوند، فرمول های اصل شمول و عدم شمول همچنان برقرار خواهد بود. به صورت کلی تر، هر دو نسخه از این اصل را می توان در چتر بزرگتر نظریه ی اندازه گیری جای داد.
در یک نگاه کاملاً انتزاعی، اصل شمول چیزی فراتر از محاسبهٔ معکوس یک ماتریس نیست. از این دیدگاه از لحاظ ریاضیاتی هیچ چیز جالبی در مورد این اصل وجود ندارد. با وجود این استفاده پذیری گستردهٔ این اصل باعث می شود که این اصل به ابزاری بسیار ارزشمند در ترکیبیات و رشته های مرتبط با آن بدل شود. آنطور که جیان کارلو روتا گفته است: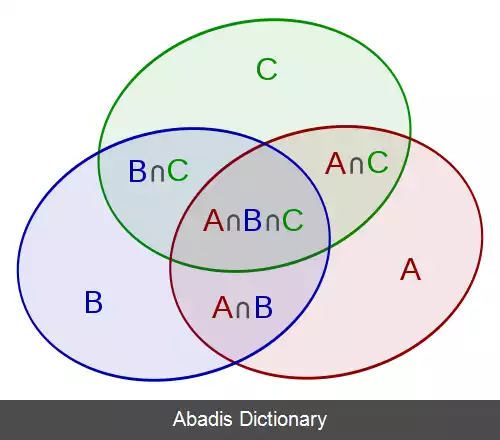
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفکه A و B دو مجموعهٔ متناهی اند و |S| نمایانگر تعداد اعضای مجموعهٔ متناهی S است. این فرمول بیان می کند که مجموع اندازهٔ دو مجموعه ممکن است بزرگتر از اندازهٔ اجتماع آن ها باشد چون بعضی از اعضا شاید دو بار شمرده شوند. اعضایی که دو بار شمرده شده اند همان اعضایی اند که در اشتراک دو مجموعه حضور دارند بنابراین با کم کردن این تعداد، اندازهٔ واقعی مجموعهٔ اجتماع بدست می آید. این اصل در حالتی که سه مجموعه داریم واضح تر دیده می شود:
این فرمول می تواند به این صورت امتحان شود که بشماریم هر ناحیه در نمودار ون چند بار در سمت راست فرمول شمرده شده است.
بسط نتایج این مثال ها اصل شمول و عدم شمول را بدست می دهد: برای یافتن اندازهٔ اجتماع n مجموعه،
• اندازهٔ هر مجموعه را اضافه کنید،
• اندازهٔ اشتراک دو به دو مجموعه ها را کم کنید،
• اندازهٔ اشتراک هر سه تایی از مجموعه ها را اضافه کنید،
• اندازهٔ اشتراک هر چهارتایی از مجموعه ها را کم کنید،
• اندازهٔ اشتراک هر پنج تایی از مجموعه ها را اضافه کنید،
• به همین صورت ادامه دهید تا زمانی که اندازهٔ اشتراک nتایی مجموعه ها اضافه ( برای n فرد ) یا کم ( برای n زوج ) شود.
این اسم از اینجا آمده که این اصل براساس یک سری شمول و عدم شمول استوار است. این مفهوم به ابراهام دو مواور ( ۱۷۱۸ ) نسبت داده می شود، ولی بار اول در مقاله ای از دنیل داسیلوا ( ۱۸۵۴ ) و بعداً در مقاله ای از جیمز جوزف سیلوستر ( ۱۸۸۳ ) ظاهر شد. به همین دلیل گاهی این اصل به عنوان فرمول داسیلوا یا سیلوستر شناخته می شود.
از آنجایی که احتمالات متناهی براساس اندازهٔ فضای احتمال محاسبه می شوند، زمانی که اندازهٔ مجموعه ها با احتمالات متناهی جایگزین می شوند، فرمول های اصل شمول و عدم شمول همچنان برقرار خواهد بود. به صورت کلی تر، هر دو نسخه از این اصل را می توان در چتر بزرگتر نظریه ی اندازه گیری جای داد.
در یک نگاه کاملاً انتزاعی، اصل شمول چیزی فراتر از محاسبهٔ معکوس یک ماتریس نیست. از این دیدگاه از لحاظ ریاضیاتی هیچ چیز جالبی در مورد این اصل وجود ندارد. با وجود این استفاده پذیری گستردهٔ این اصل باعث می شود که این اصل به ابزاری بسیار ارزشمند در ترکیبیات و رشته های مرتبط با آن بدل شود. آنطور که جیان کارلو روتا گفته است:


wiki: اصل شمول و عدم شمول
