اجماع نمونه تصادفی ( به انگلیسی: Random sample consensus ) یک روش تکرار شونده ( iterative method ) است برای تخمین پارامترهای یک مدل ریاضی روی یک مجموعه داده که شامل داده های پرت است، به طوری که داده های پرت تأثیری روی تخمینی که زده می شود نداشته باشند. با این تعریف، از این روش می توان به عنوان یک روش برای تشخیص داده پرت نیز یاد کرد. [ ۱] RANSAC در حقیقت یک الگوریتم غیرقطعی است، بدین معنا که تنها به یک احتمال مشخصی جواب مطلوب می دهد که این احتمال با افزایش تعداد دفعات اجرای الگوریتم بیشتر می شود. این الگوریتم در ابتدا توسط Fischler و Bolles در اس آرآی اینترنشنال در سال ۱۹۸۱ منتشر شد. آنها از RANSAC برای حل مسئله تعیین موقعیت ( به انگلیسی: Location Determination Problem ) استفاده کردند. در این مسئله هدف تعیین نقاطی در فضا است که نگاشت آنها روی یک تصویر بر روی مجموعه مشخصی از نقاط می افتد.
RANSAC از نمونه گیری تصادفی فرعی[ ۲] استفاده می کند. یکی از فرض های پایه ای الگوریتم این است که داده ها شامل داده درونی و داده های پرت هستند. منظور از داده های درونی، داده هایی هستند که توزیع آن ها قابل بیان توسط مجموعه ای از پارامترهای یک مدل است و البته می توانند شامل مقداری نویز باشند. داده های پرت هم داده هایی هستند که با مدل مدنظر سازگار نیستند. منشأ داده های پرت می تواند مقادیر خیلی زیاد نویز، یا اندازه گیری های خطادار ( هنگام جمع آوری داده ) یا فرض اشتباه در مورد داده ها باشد. RANSAC همچنین این فرض را دارد که با داشتن مجموعه ای ( معمولا کوچک ) از داده های درونی، فرایندی وجود دارد که با استفاده از آن می تواند پارامترهای مدلی که به صورت بهینه توزیع داده ها را بیان می کند و با داده ها سازگار است، برآورد کرد.
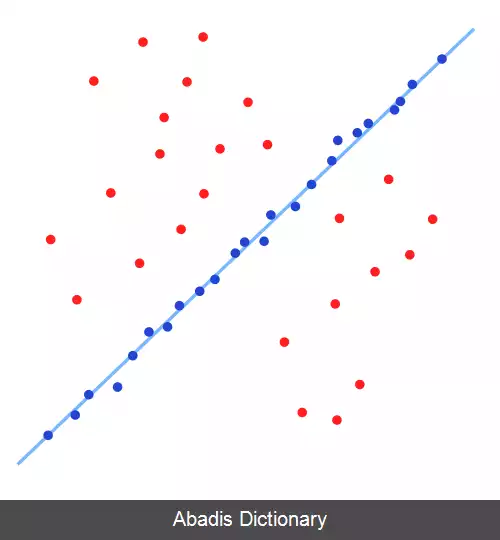
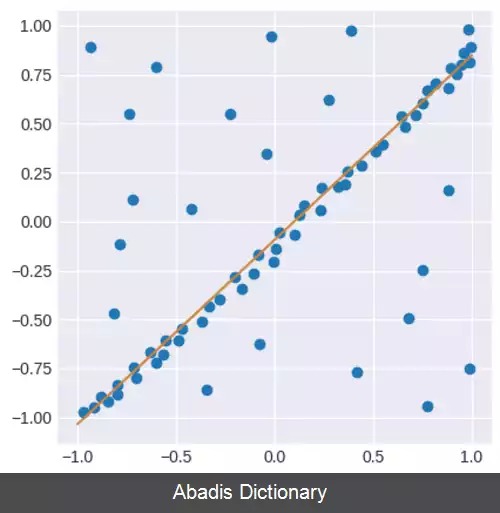
یک مثال ساده، برازش یک خط در دو بعد به یک مجموعه از مشاهدات است. با فرض اینکه این مجموعه هم شامل داده های درونی است، یعنی داده هایی که به طور تقریبی می توانند به یک خط برازش شوند، و هم داده های پرت، داده هایی که به این خط نمی توانند برازش شوند، استفاده از روش کمترین مربعات معمولی باعث می شود خطی بدست آید که به خوبی به این مجموعه داده برازش نشود. چرا که سعی شده است که این خط به همه نقاط برازش شود، که شامل داده های پرت نیز هستند. RANSAC اما سعی می کند داده های پرت را جزو داده های مورد استفاده هنگام برازش در نظر نگیرد و مدلی خطیای بیابد که هنگام برازش شدن تنها از داده های درونی استفاده می کند. این کار با برازش کردن مدل خطی به چندین زیرمجموعه از داده ها که تصادفی انتخاب شده اند و انتخاب مدلی که بهترین برازش را به زیرمجموعه ای از داده ها داشته است، انجام می شود. از آنجا که داده های درونی نسبت به مخلوطی تصادفی از داده های درونی و داده های پرت، بیشتر به صورت خطی به هم مرتبط هستند، زیرمجموعه تصادفی ای که به صورت کامل از داده های درونی تشکیل شده باشد، بهترین برازش مدل خطی را حاصل می شود. در عمل، هیچ تضمینی وجود ندارد که زیرمجموعه ای انتخاب شود که تنها شامل داده های درونی باشد و احتمال موفقیت الگوریتم به نسبت داده های درونی به کل داده ها و انتخاب پارامترهای الگوریتم بستگی دارد.
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفRANSAC از نمونه گیری تصادفی فرعی[ ۲] استفاده می کند. یکی از فرض های پایه ای الگوریتم این است که داده ها شامل داده درونی و داده های پرت هستند. منظور از داده های درونی، داده هایی هستند که توزیع آن ها قابل بیان توسط مجموعه ای از پارامترهای یک مدل است و البته می توانند شامل مقداری نویز باشند. داده های پرت هم داده هایی هستند که با مدل مدنظر سازگار نیستند. منشأ داده های پرت می تواند مقادیر خیلی زیاد نویز، یا اندازه گیری های خطادار ( هنگام جمع آوری داده ) یا فرض اشتباه در مورد داده ها باشد. RANSAC همچنین این فرض را دارد که با داشتن مجموعه ای ( معمولا کوچک ) از داده های درونی، فرایندی وجود دارد که با استفاده از آن می تواند پارامترهای مدلی که به صورت بهینه توزیع داده ها را بیان می کند و با داده ها سازگار است، برآورد کرد.
یک مثال ساده، برازش یک خط در دو بعد به یک مجموعه از مشاهدات است. با فرض اینکه این مجموعه هم شامل داده های درونی است، یعنی داده هایی که به طور تقریبی می توانند به یک خط برازش شوند، و هم داده های پرت، داده هایی که به این خط نمی توانند برازش شوند، استفاده از روش کمترین مربعات معمولی باعث می شود خطی بدست آید که به خوبی به این مجموعه داده برازش نشود. چرا که سعی شده است که این خط به همه نقاط برازش شود، که شامل داده های پرت نیز هستند. RANSAC اما سعی می کند داده های پرت را جزو داده های مورد استفاده هنگام برازش در نظر نگیرد و مدلی خطیای بیابد که هنگام برازش شدن تنها از داده های درونی استفاده می کند. این کار با برازش کردن مدل خطی به چندین زیرمجموعه از داده ها که تصادفی انتخاب شده اند و انتخاب مدلی که بهترین برازش را به زیرمجموعه ای از داده ها داشته است، انجام می شود. از آنجا که داده های درونی نسبت به مخلوطی تصادفی از داده های درونی و داده های پرت، بیشتر به صورت خطی به هم مرتبط هستند، زیرمجموعه تصادفی ای که به صورت کامل از داده های درونی تشکیل شده باشد، بهترین برازش مدل خطی را حاصل می شود. در عمل، هیچ تضمینی وجود ندارد که زیرمجموعه ای انتخاب شود که تنها شامل داده های درونی باشد و احتمال موفقیت الگوریتم به نسبت داده های درونی به کل داده ها و انتخاب پارامترهای الگوریتم بستگی دارد.



wiki: اجماع نمونه تصادفی
