اتصال چنبره ای

اتصال چنبره ای یک توپولوژی شبکه بدون سوئیچ برای اتصال گره های پردازنده در یک سیستم کامپیوتری موازی است.
در هندسه، یک چنبره با چرخش یک دایره حول محوری هم سطح با دایره ایجاد می شود. با وجود اینکه این یک تعریف کلی در هندسه است، ویژگی های توپولوژیکی این نوع شکل، توپولوژی شبکه را در ذات خود توصیف می کند.
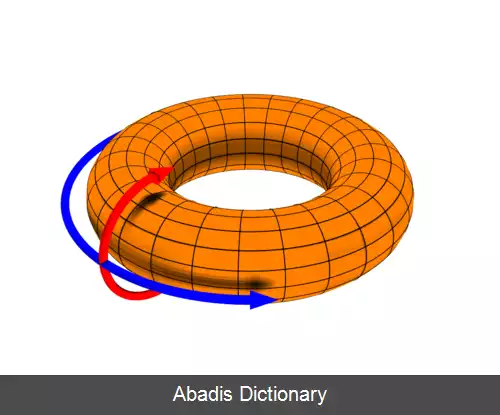
تصاویر زیر چنبره های یک بعدی و دو بعدی را نشان می دهند. چنبره یک بعدی یک دایره ساده است و چنبره دو بعدی به شکل یک دونات است. انیمیشن زیر نشان می دهد که چگونه یک چنبره دو بعدی از یک مستطیل با اتصال دو جفت لبه مقابل آن ایجاد می شود. در اینجا مفهوم چنبره برای توصیف اینکه اساساً شروع و پایان یک دنباله از گره ها به هم متصل شده است، مانند یک دونات استفاده می شود. برای تشریح بهتر مفهوم و درک اینکه توپولوژی در اتصال شبکه به چه معناست، سه مثال از گره های موازی به هم پیوسته با استفاده از توپولوژی چنبره ارائه می دهیم. در یک بعد، توپولوژی چنبره معادل یک شبکه اتصال حلقه ای به شکل دایره است. در حالت دو بعدی، معادل مش دو بعدی است، اما با اتصال اضافی در گره های لبه، که تعریف چنبره دو بعدی است.
از روی اشکال بالا می توانیم قاعده را تعمیم دهیم. اتصال چنبره ای یک توپولوژی بدون سوئیچ است که می تواند به عنوان یک اتصال شبکه توری با گره هایی که در یک آرایه مستطیلی با ابعاد N = ۲، ۳ یا بیشتر چیده شده اند، به همراه پردازنده های متصل به نزدیکترین همسایگان خود و پردازنده های متناظر متصل در لبه های مقابل آرایه دیده شود. در این شبکه، هر گره دارای 2N اتصال است. این توپولوژی نام خود را از این واقعیت گرفته است که شبکه تشکیل شده در این روش از نظر توپولوژیکی با یک چنبره N - بعدی همگن است.
تجسم سه بعد اول توپولوژی شبکه چنبره ای راحت تر است و در زیر توضیح داده شده:
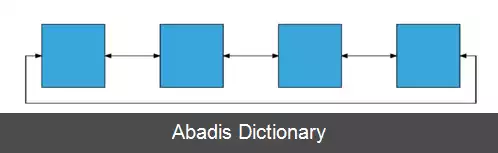
• چنبره یک بعدی: فقط یک بعد داریم، n گره در حلقه ای بسته به هم متصل می شوند که هر گره به دو همسایه نزدیکتر خود متصل است، ارتباط می تواند در دو جهت x+ و x - انجام شود. چنبره یک بعدی همان اتصال حلقوی است.
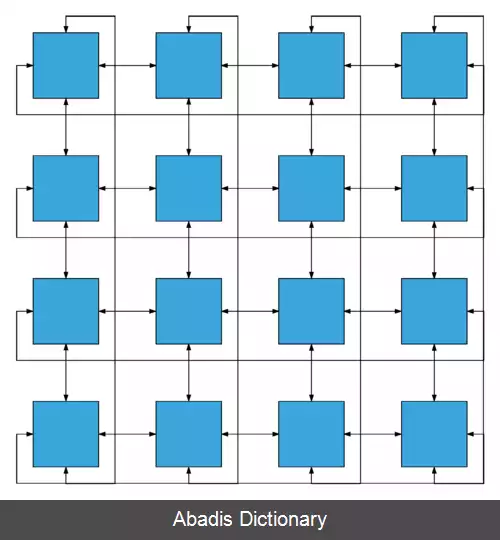
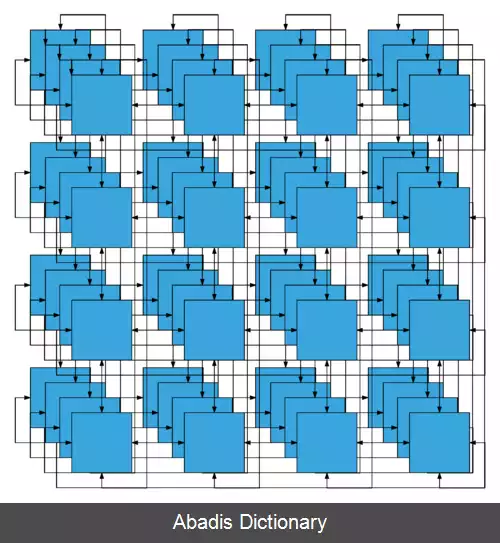
• چنبره دوبعدی: دو بعد با درجه ۴ است، گره ها در یک شبکه مستطیلی دو بعدی متشکل از n ردیف و n ستون تصور می شوند که هر گره به چهار همسایه نزدیکتر خود متصل است و گره های متناظر در لبه های مقابل به هم متصل هستند. اتصال لبه های مخالف را می توان با چرخاندن آرایه مستطیلی به شکل یک «لوله» برای اتصال دو لبه مخالف و سپس خم کردن «لوله» به شکل یک چنبره برای اتصال دو لبه دیگر تجسم کرد. ارتباط می تواند در چهار جهت +x، −x, +y و −y انجام شود. مجموع گره های چنبره دوبعدی n 2 است.
• چنبره سه بعدی: سه بعد دارد، گره ها در یک شبکه سه بعدی به شکل یک منشور مستطیلی تصور می شوند که هر گره به ۶ همسایه خود متصل است و گره های متناظر در وجوه مقابل آرایه متصل هستند. هر لبه از n گره تشکیل شده است. ارتباط می تواند در ۶ جهت انجام شود، +x، −x, +y، −y, +z، −z. هر لبه چنبره سه بعدی از n گره تشکیل شده است. مجموع گره های چنبره سه بعدی n 3 است.
• چنبره N بعدی: می تواند N بعد داشته باشد، هر گره از چنبره N بعدی دارای 2N همسایه است، ارتباط می تواند در جهت 2N جهت انجام شود. هر لبه از n گره تشکیل شده است. مجموع گره های این چنبره n N است. انگیزه اصلی داشتن ابعاد بالاتر چنبره، دستیابی به پهنای باند بالاتر، تأخیر کمتر و مقیاس پذیری بالاتر است.