ابربیضی که به یاد گابریل لامه با نام منحنی لامه نیز شناخته می شود، منحنی بسته ای مشابه بیضی است که جنبه های هندسی آن شامل نیم قطر بزرگ، نیم قطر کوچک و تقارن حول آنها را حفظ می کند، ولی شکل کلی متفاوتی دارد.
در دستگاه مختصات دکارتی، مجموعه نقاط روی منحنی معادلهٔ زیر را ارضا می کنند:
که در آن n و a و b اعدادی مثبت هستند و خط های عمودی پیرامون یک عدد، قدر مطلق آن را نشان می دهند.
این فرمول به تعریف منحنی بسته ای می پردازد که در مستطیلی به ابعاد 2a و 2b محاط است. پارامترهای a و b را نیم قطرهای منحنی می نامند.
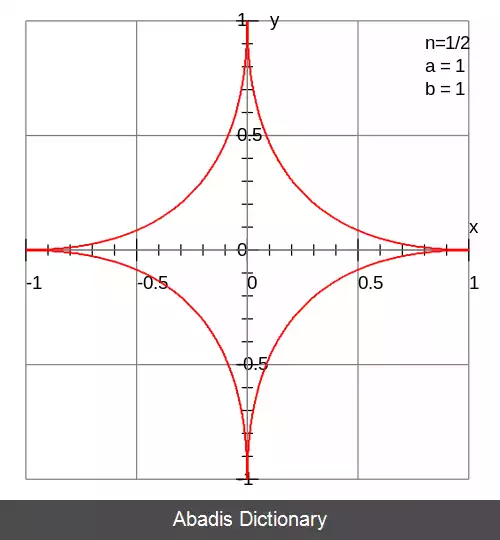
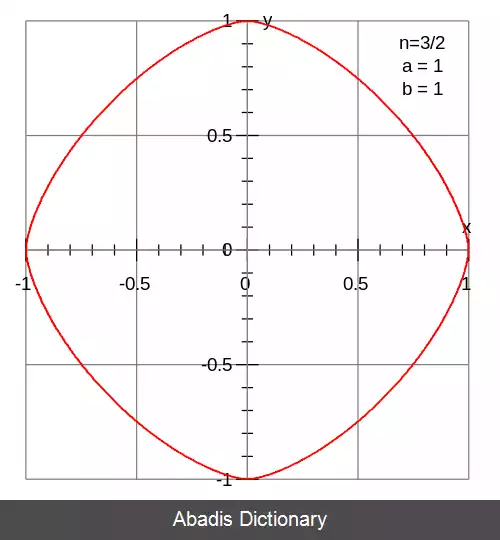
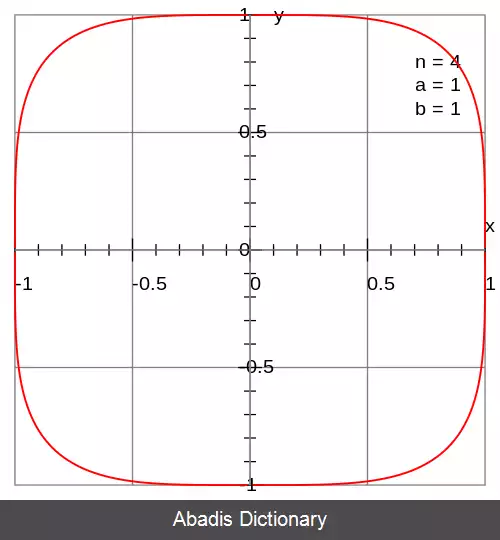
اگر n عدد گویای مثبتی به شکل p/q باشد، هر ربع ابربیضی منحنی جبری از مرتبهٔ pq است. [ ۱] در حالت خاص a=b=۱ و n زوج، منحنی فرما از درجهٔ n خواهد بود. اگر صورت کسر زوج نباشد، منحنی از اجزای منحنی جبری مشابهی در راستاهای مختلف تشکیل می شود.
می توان منحنی را با معادلات پارامتری زیر ( که پارامتر t تفسیر هندسی ندارد ) توصیف کرد:
به ازای هر مقدار t چهار نقطه روی منحنی مشخص می شود. معادل آن می توان برای t در بازهٔ 0 ≤ t < 2 π تعریف کرد:
که در آن تابع علامت به صورت زیر تعریف می شود:
می توان مساحت ابربیضی را برحسب تابع گاما بیان کرد: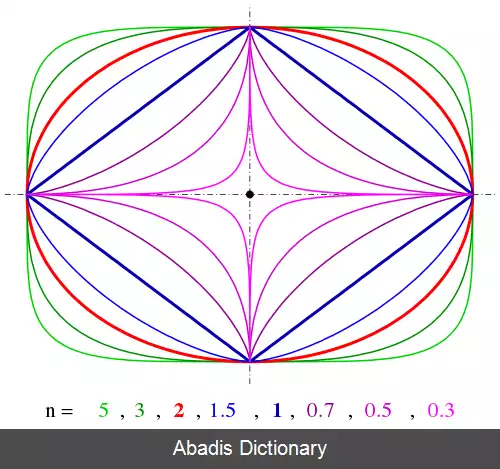
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر دستگاه مختصات دکارتی، مجموعه نقاط روی منحنی معادلهٔ زیر را ارضا می کنند:
که در آن n و a و b اعدادی مثبت هستند و خط های عمودی پیرامون یک عدد، قدر مطلق آن را نشان می دهند.
این فرمول به تعریف منحنی بسته ای می پردازد که در مستطیلی به ابعاد 2a و 2b محاط است. پارامترهای a و b را نیم قطرهای منحنی می نامند.
اگر n عدد گویای مثبتی به شکل p/q باشد، هر ربع ابربیضی منحنی جبری از مرتبهٔ pq است. [ ۱] در حالت خاص a=b=۱ و n زوج، منحنی فرما از درجهٔ n خواهد بود. اگر صورت کسر زوج نباشد، منحنی از اجزای منحنی جبری مشابهی در راستاهای مختلف تشکیل می شود.
می توان منحنی را با معادلات پارامتری زیر ( که پارامتر t تفسیر هندسی ندارد ) توصیف کرد:
به ازای هر مقدار t چهار نقطه روی منحنی مشخص می شود. معادل آن می توان برای t در بازهٔ 0 ≤ t < 2 π تعریف کرد:
که در آن تابع علامت به صورت زیر تعریف می شود:
می توان مساحت ابربیضی را برحسب تابع گاما بیان کرد:




wiki: ابربیضی
