T sne کاهش ابعاد داده. t - SNE یک الگوریتم تجزیه و تحلیل داده های چند بعدی است که برای تصویرسازی داده ها در فضایی با بعد کمتر ( عموما دو بعدی یا سه بعدی ) استفاده می شود و اولین بار، توسط لورنس ون در ماتن و جفری هینتون در سال ۲۰۰۸ معرفی شده است[ ۱] [ ۲] .
با استفاده از t - SNE، می توان داده های پیچیده و چند بعدی را به صورت یکنواخت و منظم در فضای کاهش یافته نشان داد. این الگوریتم باعث ایجاد فضای جدیدی می شود که در آن داده های مشابه به هم نزدیک و داده های متفاوت از هم دور قرار می گیرند. به عبارت دیگر، داده هایی که در فضای اصلی به هم نزدیک بودند، در فضای کاهش یافته نیز به هم نزدیک باقی می مانند و داده هایی که در فضای اصلی دور از هم بودند، در فضای کاهش یافته نیز دور از هم قرار می گیرند.
t - SNE برای تصویرسازی داده هایی که به صورت غیرخطی در فضای چند بعدی نشان داده می شوند، بسیار مناسب است. این الگوریتم برای کاهش ابعاد داده های پیچیده، مانند تصاویر و داده های صوتی، نیز کارآمد است.
در کل، t - SNE یک الگوریتم کارآمد و مفید برای تصویرسازی داده هاست که به صورت گسترده در حوزه های مختلف مانند علم داده، بینایی ماشین، آمار، ژنومیک، امنیت سایبری، پردازش زبان طبیعی، تحلیل موسیقی، تحقیقات سرطان، بیوانفورماتیک، تفسیر ژئولوژی، و پردازش سیگنال های پزشکی و . . . استفاده می شود.
این الگوریتم با محاسبه ماتریس شباهت بین داده های مختلف ( به صورت پیش فرض بر اساس فاصله اقلیدسی ) ، شروع به کاهش ابعاد داده ها می کند و با استفاده از توزیع احتمال برای جفت داده ها در فضای بالا بعد و فضای پایین بعد، کاهش بعد را انجام می دهد. سپس با کمینه کردن فاصله بین این دو توزیع احتمال با استفاده از الگوریتم گرادیان کاهشی، سعی در حفظ ساختار محلی فضای بالا بعد اصلی دارد.
نتیجه ی این الگوریتم، نمایشی بهتر و کاهش بعد داده ها در فضای پایین بعد است. داده هایی که در فضای بالا بعد به هم نزدیک بوده اند، در فضای پایین بعد نیز به هم نزدیک باقی خواهند ماند و داده هایی که در فضای بالا بعد دور از هم بوده اند، در فضای پایین بعد نیز دور از هم خواهند بود.
یکی از مزایای t - SNE، توانایی آن در درک روابط غیرخطی بین داده ها است که این الگوریتم را برای تصویرسازی داده های پیچیده مانند تصاویر و فایل های صوتی مناسب می سازد. با این حال، این الگوریتم پردازشی هزینه بر است و نیاز به تنظیم دقیق پارامترهای آن دارد تا نتایج بهتری حاصل شود.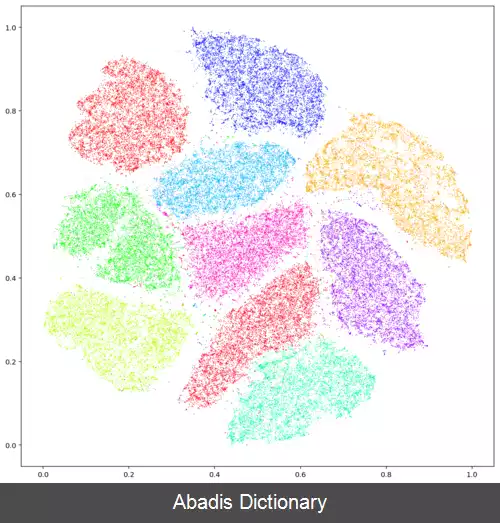
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبا استفاده از t - SNE، می توان داده های پیچیده و چند بعدی را به صورت یکنواخت و منظم در فضای کاهش یافته نشان داد. این الگوریتم باعث ایجاد فضای جدیدی می شود که در آن داده های مشابه به هم نزدیک و داده های متفاوت از هم دور قرار می گیرند. به عبارت دیگر، داده هایی که در فضای اصلی به هم نزدیک بودند، در فضای کاهش یافته نیز به هم نزدیک باقی می مانند و داده هایی که در فضای اصلی دور از هم بودند، در فضای کاهش یافته نیز دور از هم قرار می گیرند.
t - SNE برای تصویرسازی داده هایی که به صورت غیرخطی در فضای چند بعدی نشان داده می شوند، بسیار مناسب است. این الگوریتم برای کاهش ابعاد داده های پیچیده، مانند تصاویر و داده های صوتی، نیز کارآمد است.
در کل، t - SNE یک الگوریتم کارآمد و مفید برای تصویرسازی داده هاست که به صورت گسترده در حوزه های مختلف مانند علم داده، بینایی ماشین، آمار، ژنومیک، امنیت سایبری، پردازش زبان طبیعی، تحلیل موسیقی، تحقیقات سرطان، بیوانفورماتیک، تفسیر ژئولوژی، و پردازش سیگنال های پزشکی و . . . استفاده می شود.
این الگوریتم با محاسبه ماتریس شباهت بین داده های مختلف ( به صورت پیش فرض بر اساس فاصله اقلیدسی ) ، شروع به کاهش ابعاد داده ها می کند و با استفاده از توزیع احتمال برای جفت داده ها در فضای بالا بعد و فضای پایین بعد، کاهش بعد را انجام می دهد. سپس با کمینه کردن فاصله بین این دو توزیع احتمال با استفاده از الگوریتم گرادیان کاهشی، سعی در حفظ ساختار محلی فضای بالا بعد اصلی دارد.
نتیجه ی این الگوریتم، نمایشی بهتر و کاهش بعد داده ها در فضای پایین بعد است. داده هایی که در فضای بالا بعد به هم نزدیک بوده اند، در فضای پایین بعد نیز به هم نزدیک باقی خواهند ماند و داده هایی که در فضای بالا بعد دور از هم بوده اند، در فضای پایین بعد نیز دور از هم خواهند بود.
یکی از مزایای t - SNE، توانایی آن در درک روابط غیرخطی بین داده ها است که این الگوریتم را برای تصویرسازی داده های پیچیده مانند تصاویر و فایل های صوتی مناسب می سازد. با این حال، این الگوریتم پردازشی هزینه بر است و نیاز به تنظیم دقیق پارامترهای آن دارد تا نتایج بهتری حاصل شود.

wiki: T sne کاهش ابعاد داده
