اعداد طبیعی یا اعداد صحیح مثبت[ ۱] اعدادی هستند که از یک شروع می شود و تا بینهایت ( عدد n ) ادامه دارند. و شامل صفر نمی شود و برای شمارش ( به طور مثال در «شش سکه روی میز است» ) و برای ترتیب ( به طور مثال در «این سومین شهر بزرگ در کشور است» ) به کار می روند. در اصطلاح شناسی ریاضیات، لغت مورد استفاده برای شمارش اشیاء واقعی «اعداد ترتیبی» است. مجموعهٔ اعداد طبیعی همان مجموعهٔ اعداد صحیح مثبت یعنی {. . . و۱٬۲٬۳} است. این اعداد شامل اعداد مرکب، اعداد اول و یک است.
به بیان ساده، عدد طبیعی، عددی است که در طبیعت وجود دارد و برای شمردن عناصر طبیعی استفاده می شوند، برای مثال عدد صفر یا اعداد منفی در طبیعت وجود ندارند و در مجموعه اعداد طبیعی نیستند.
برای بودن یا نبودن عدد صفر در مجموعه اعداد طبیعی سه تعریف موجود می باشد. در تعریف اول طبق استاندارد ISO 80000 - 2 عدد صفر با عنوان اعداد صحیح غیر منفی پذیرفته شده است. [ ۲] اما در تعریف دیگر صفر به عنوان یک عضو شناخته نمی شود و با اضافه کردن آن، مجموعه اعداد حسابی به وجود می آید. این مجموعه یک مجموعه نامتناهی است. پس تنها تفاوت بین اعداد طبیعی و اعداد حسابی وجود صفر در اعداد حسابی است. در ریاضیات اعداد صحیح و حسابی را نیز به ترتیب با حروف Z و W نمایش می دهند. N از حرف آغاز واژه انگلیسی Natural، به معنای نهادی ( طبیعی ) ، گرفته شده است. باور فعلی علم بر آن است که صفر یک عدد بی علامت است که جزء اعداد صحیح و حسابی می باشد. مجموعۀ اعداد طبیعی، یک مجموعۀ نامتناهی است و زیر مجموعه ی اعداد حسابی، اعداد صحیح، اعداد گویا و اعداد حقیقی می باشد.
بنیادی ترین ویژگی اعداد طبیعی اصل استقرای ریاضی است. استقرار ریاضی بیان می کند که اگر P ( x ) به معنای صدق ویژگی P برای عدد x باشد، برای اینکه P ( x ) برای همهٔ اعداد طبیعی صدق کند باید:[ ۳]
• P ( 1 ) {\displaystyle P ( 1 ) } صدق کند، و
• با فرض اینکه P ( k ) {\displaystyle P ( k ) } صدق می کند بتوان ثابت کرد P ( k + 1 ) {\displaystyle P ( k+1 ) } نیز صادق است.
به این ترتیب با ترکیب شرط ۱ و ۲ ( در حالت خاص k = 1 ) می توان گفت که P ( 2 ) هم صادق است، در نتیجه بنابر شرط ۲ ( در حالت خاص k = 2 ) ، P ( 3 ) هم صادق است. واضح است که با تکرار چندبارهٔ این عملیات می توان ویژگی P را برای هر عددی ثابت کرد، ازین رو P ( k ) برای همهٔ اعداد k صادق است. [ ۴]

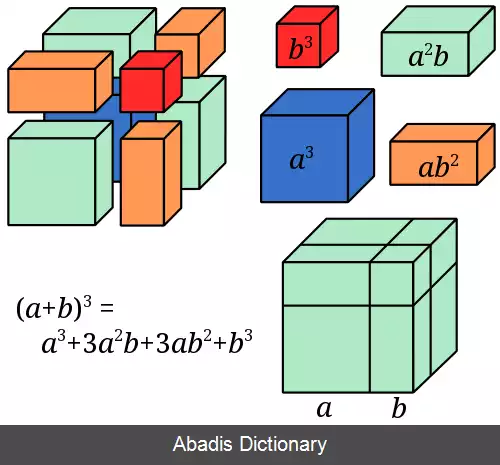
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفبه بیان ساده، عدد طبیعی، عددی است که در طبیعت وجود دارد و برای شمردن عناصر طبیعی استفاده می شوند، برای مثال عدد صفر یا اعداد منفی در طبیعت وجود ندارند و در مجموعه اعداد طبیعی نیستند.
برای بودن یا نبودن عدد صفر در مجموعه اعداد طبیعی سه تعریف موجود می باشد. در تعریف اول طبق استاندارد ISO 80000 - 2 عدد صفر با عنوان اعداد صحیح غیر منفی پذیرفته شده است. [ ۲] اما در تعریف دیگر صفر به عنوان یک عضو شناخته نمی شود و با اضافه کردن آن، مجموعه اعداد حسابی به وجود می آید. این مجموعه یک مجموعه نامتناهی است. پس تنها تفاوت بین اعداد طبیعی و اعداد حسابی وجود صفر در اعداد حسابی است. در ریاضیات اعداد صحیح و حسابی را نیز به ترتیب با حروف Z و W نمایش می دهند. N از حرف آغاز واژه انگلیسی Natural، به معنای نهادی ( طبیعی ) ، گرفته شده است. باور فعلی علم بر آن است که صفر یک عدد بی علامت است که جزء اعداد صحیح و حسابی می باشد. مجموعۀ اعداد طبیعی، یک مجموعۀ نامتناهی است و زیر مجموعه ی اعداد حسابی، اعداد صحیح، اعداد گویا و اعداد حقیقی می باشد.
بنیادی ترین ویژگی اعداد طبیعی اصل استقرای ریاضی است. استقرار ریاضی بیان می کند که اگر P ( x ) به معنای صدق ویژگی P برای عدد x باشد، برای اینکه P ( x ) برای همهٔ اعداد طبیعی صدق کند باید:[ ۳]
• P ( 1 ) {\displaystyle P ( 1 ) } صدق کند، و
• با فرض اینکه P ( k ) {\displaystyle P ( k ) } صدق می کند بتوان ثابت کرد P ( k + 1 ) {\displaystyle P ( k+1 ) } نیز صادق است.
به این ترتیب با ترکیب شرط ۱ و ۲ ( در حالت خاص k = 1 ) می توان گفت که P ( 2 ) هم صادق است، در نتیجه بنابر شرط ۲ ( در حالت خاص k = 2 ) ، P ( 3 ) هم صادق است. واضح است که با تکرار چندبارهٔ این عملیات می توان ویژگی P را برای هر عددی ثابت کرد، ازین رو P ( k ) برای همهٔ اعداد k صادق است. [ ۴]



wiki: عدد طبیعی
