دو گراف که تعداد یکسانی رأس دارند و این رأس ها نیز به صورت مشابهی به یکدیگر متصل گشته اند، یکریخت نامیده می شوند.
دو گراف یکریخت اند اگر و فقط اگر تابعی یک به یک و پوشا به صورت f : V ( G ) → V ( H ) بین مجموعه رئوس دو گراف G و H وجود داشته باشد به طوری که u v ∈ E ( G ) ، اگر و فقط اگر f ( u ) f ( v ) ∈ E ( H ) . در این صورت دو گراف G و H را یکریخت گویند و می نویسند: G ≅ H . [ ۱]
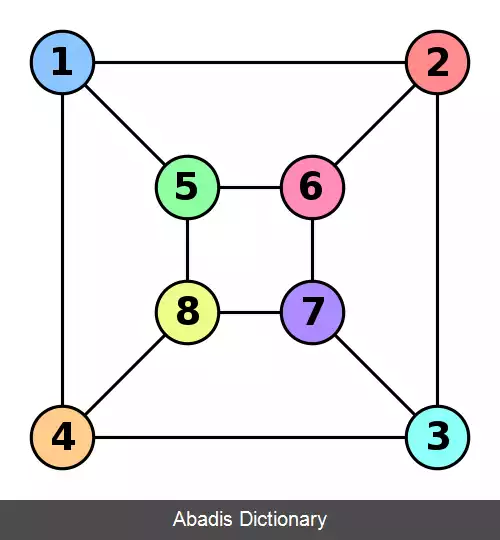
دو گراف زیر با این که ظاهر متفاوتی دارند اما با هم یکریختند.
برای تعیین یکریخی دو گراف باید به چند مورد توجه شود:
• تعداد رئوس
• تعداد یال ها
• درجهٔ هر یک از رئوس
• همسایگی هر راس
برای مثال در شکل نشان داده شده این دو گراف یک ریخت اند.
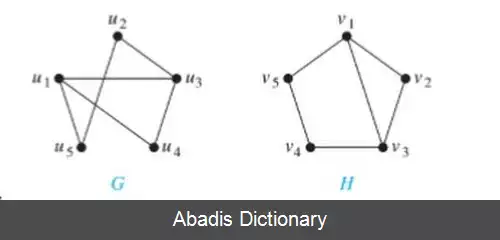
بعد از مشاهده تعداد یال ها، راس ها، درجهٔ هر راس و نظیر کردن دو گراف به یکدیگر، می گوییم این دو گراف شرایط هم ریختی را دارند. ( شرط لازم ) اکنون باید هر راس گراف به دیگری نظیر شود. برای مثال در گراف رو برو: راس u1 دارای درجهٔ ۳ است، با دو راس درجهٔ ۲ ( یعنی u5 و u4 ) و با یک راس درجهٔ ۳ ( یعنی u3 ) همسایه است. نظیر این راس در گراف H می تواند راس v1 باشد چون این راس دقیقاً همهٔ خصوصیات راس u1 را دارد. همین مسیر را ادامه می دهیم. اگر در پایان کار مشاهده شد که همهٔ راس ها در دو گراف دو به دو نظیر اند می گوییم این دو گراف یک ریخت اند. ( شرط کافی )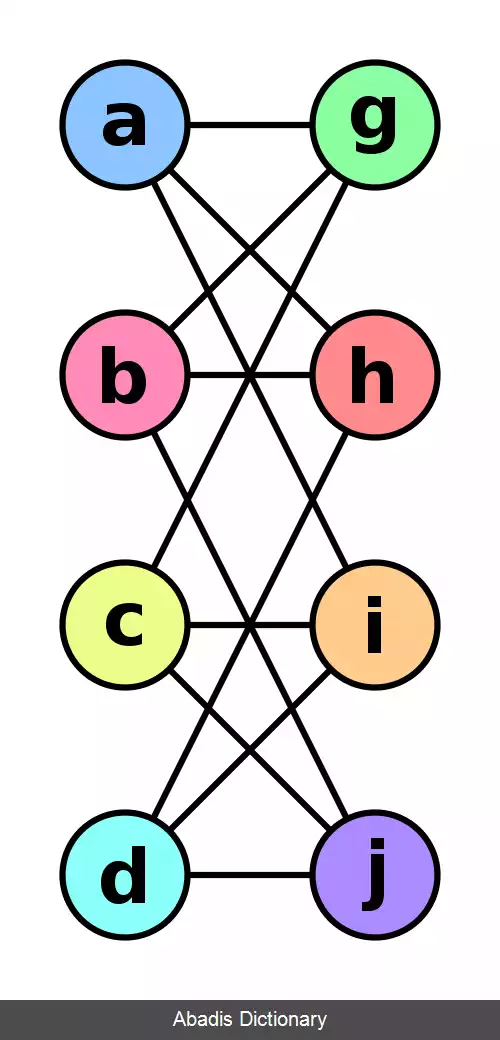
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدو گراف یکریخت اند اگر و فقط اگر تابعی یک به یک و پوشا به صورت f : V ( G ) → V ( H ) بین مجموعه رئوس دو گراف G و H وجود داشته باشد به طوری که u v ∈ E ( G ) ، اگر و فقط اگر f ( u ) f ( v ) ∈ E ( H ) . در این صورت دو گراف G و H را یکریخت گویند و می نویسند: G ≅ H . [ ۱]
دو گراف زیر با این که ظاهر متفاوتی دارند اما با هم یکریختند.
برای تعیین یکریخی دو گراف باید به چند مورد توجه شود:
• تعداد رئوس
• تعداد یال ها
• درجهٔ هر یک از رئوس
• همسایگی هر راس
برای مثال در شکل نشان داده شده این دو گراف یک ریخت اند.
بعد از مشاهده تعداد یال ها، راس ها، درجهٔ هر راس و نظیر کردن دو گراف به یکدیگر، می گوییم این دو گراف شرایط هم ریختی را دارند. ( شرط لازم ) اکنون باید هر راس گراف به دیگری نظیر شود. برای مثال در گراف رو برو: راس u1 دارای درجهٔ ۳ است، با دو راس درجهٔ ۲ ( یعنی u5 و u4 ) و با یک راس درجهٔ ۳ ( یعنی u3 ) همسایه است. نظیر این راس در گراف H می تواند راس v1 باشد چون این راس دقیقاً همهٔ خصوصیات راس u1 را دارد. همین مسیر را ادامه می دهیم. اگر در پایان کار مشاهده شد که همهٔ راس ها در دو گراف دو به دو نظیر اند می گوییم این دو گراف یک ریخت اند. ( شرط کافی )



wiki: یک ریختی گراف
