در ریاضیات، گروه دووجهی نامتناهی یک گروه نامتناهی با ویژگی های مشابه گروه دووجهی متناهی است.
در هندسه اقلیدسی، گروه دووجهی نامتناهی، تقارن گروه فرایز ( خط های تکرار شونده موازی ) را نشان می دهد. در تصویر روبه رو p1m۱، به عنوان مجموعه ای نامتناهی از بازتاب های موازی در امتداد یک محور دیده می شود.
یک گروه دووجهی، با یکبار چرخش r و یکبار بازتاب ایجاد می شود. اگر چرخشی مضربی گویا و غیرگنگ چرخش کاملی باشد، آنگاه هر چند n صحیحی وجود داشته باشد، rn هویت وی خواهد بود و ما یک گروه نامتناهی دووجهی از مرتبه ۲n خواهیم داشت. اگر چرخش مضرب گویای چرخشی کامل نباشد، چنین nی وجود ندارد و گروه به دست آمده، عناصر نامتناهی زیادی خواهد داشت و گروه نامتناهی دووجهی نامیده می شود.
ارائه ان به این صورت است: ⟨ r , s ∣ s 2 = 1 , s r s = r − 1 ⟩ [ ۱] ⟨ x , y ∣ x 2 = y 2 = 1 ⟩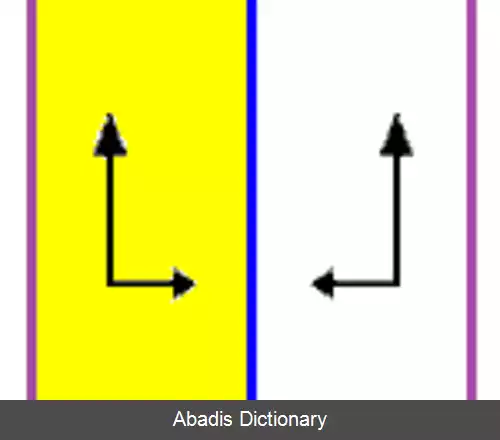
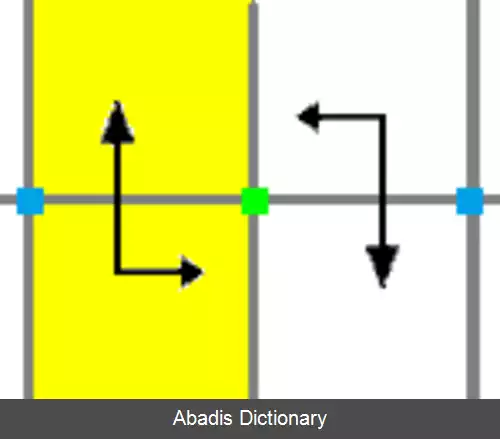
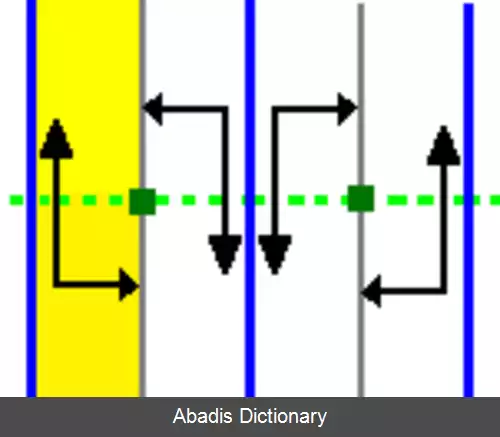
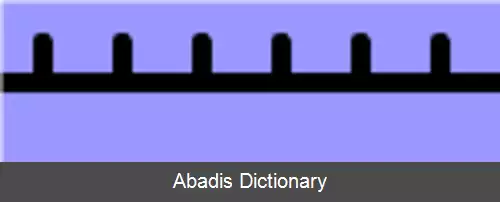


این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر هندسه اقلیدسی، گروه دووجهی نامتناهی، تقارن گروه فرایز ( خط های تکرار شونده موازی ) را نشان می دهد. در تصویر روبه رو p1m۱، به عنوان مجموعه ای نامتناهی از بازتاب های موازی در امتداد یک محور دیده می شود.
یک گروه دووجهی، با یکبار چرخش r و یکبار بازتاب ایجاد می شود. اگر چرخشی مضربی گویا و غیرگنگ چرخش کاملی باشد، آنگاه هر چند n صحیحی وجود داشته باشد، rn هویت وی خواهد بود و ما یک گروه نامتناهی دووجهی از مرتبه ۲n خواهیم داشت. اگر چرخش مضرب گویای چرخشی کامل نباشد، چنین nی وجود ندارد و گروه به دست آمده، عناصر نامتناهی زیادی خواهد داشت و گروه نامتناهی دووجهی نامیده می شود.
ارائه ان به این صورت است: ⟨ r , s ∣ s 2 = 1 , s r s = r − 1 ⟩ [ ۱] ⟨ x , y ∣ x 2 = y 2 = 1 ⟩






wiki: گروه دووجهی بی نهایت
