در علم کامپیوتر نظری و تئوری زبان رسمی، یک گِرامر درخت منظم، گرامر صوری است که مجموعه ای از درختان جهت دار یا جملات ( terms ) را توصیف می کند. گرامر کلمه منظم می تواند به عنوان یک نوع خاص از گرامر درخت منظم که مجموعه ای از درختان تک مسیر را توصیف می کند بیان شود.
گرامر درخت منظم توسط چندتایی
( G = ( N, Σ, Z, P
که در آن
• N مجموعه ای از غیرپایانه ها
• Σ الفبای رتبه ای مجزا شده از N
• Z یک غیرپایانه شروع است به طوریکه Z ∈ N و
• P مجموعه ای از انتقالات به فرم A → t که A ∈ N و ( t ∈ TΣ ( N به صورتی که
( TΣ ( N جبر واژه همراه است، یعنی مجموعه ای از تمام درختان تشکیل شده از نمادها در Σ ∪ N با توجه به arities خود که در آن غیر پایانه ها nullary در نظر گرفته می شود.
دستور زبان G به طور ضمنی مجموعه ای از درختان تعرف می شود : هر درختی که می تواند از Z با استفاده از مجموعهٔ قوانین P مشتق شود ، گفته می شود که توسط G توصیف شده است .
این مجموعه از درختان به عنوان زبان G شناخته می شوند . به طور رسمی تر ، رابطهٔ ⇒G روی مجموعهٔ ( TΣ ( N به صورت زیر تعرف می شود :
درخت ( t1∈ TΣ ( N می تواند در یک مرحله اشتقاق شود به درخت ( t1∈ TΣ ( N اگر وجود داشته باشد : متن S و انتقال A→t ) ∈ P ) به طوری که
• [t1 = S[A و
• [t2 = S[t.
در اینجا یک بافت ( متن ) به معنی یک درخت با دقیقاً یک حفره در آن است و [S[t نشان دهندهٔ نتیجهٔ پر کردن درخت T با حفره ای از S است .
زبان درخت تولید شده توسط T زبان { L ( G ) = { t ∈ TΣ | Z ⇒G* t است.
در اینجا TΣ نشان دهندهٔ مجموعه ای از تمام درختان تشکیل شده از نمادهای Σ , درحالیکه ⇒G* نشان دهندهٔ عملیات پی در پی از ⇒G است.
فرض کنید G1 = ( N1, Σ1 ) , Z1 , P1 که در آن
• {N1 = {Bool, BList مجموعه ای از غیرپایانه های ماست.
• {N1 = {Bool, BList الفبای رتبه بندی شدهٔ ماست که arities توسط استدلال های ساختگی نشان داده شده ( یعنی منفی نماد arity 2 است )
• Z1 = BList غیرپایانه آغازین است و
• مجموعهٔ P1 شامل موارد زیر می شود:
• Bool → false
• Bool → true
• BList → nil
• ( BList → cons ( Bool, BList
مثالی از اشتقاق گرامر G1 :
BList ⇒ cons ( Bool, BList ) ⇒ cons ( false, cons ( Bool, BList ) ) ⇒ cons ( false, cons ( true, nil ) )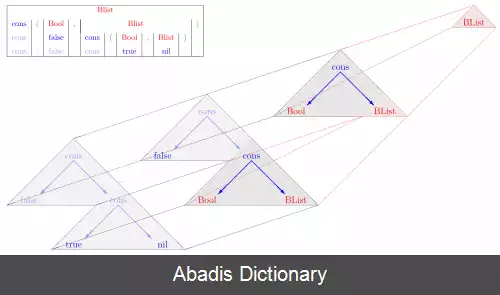
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفگرامر درخت منظم توسط چندتایی
( G = ( N, Σ, Z, P
که در آن
• N مجموعه ای از غیرپایانه ها
• Σ الفبای رتبه ای مجزا شده از N
• Z یک غیرپایانه شروع است به طوریکه Z ∈ N و
• P مجموعه ای از انتقالات به فرم A → t که A ∈ N و ( t ∈ TΣ ( N به صورتی که
( TΣ ( N جبر واژه همراه است، یعنی مجموعه ای از تمام درختان تشکیل شده از نمادها در Σ ∪ N با توجه به arities خود که در آن غیر پایانه ها nullary در نظر گرفته می شود.
دستور زبان G به طور ضمنی مجموعه ای از درختان تعرف می شود : هر درختی که می تواند از Z با استفاده از مجموعهٔ قوانین P مشتق شود ، گفته می شود که توسط G توصیف شده است .
این مجموعه از درختان به عنوان زبان G شناخته می شوند . به طور رسمی تر ، رابطهٔ ⇒G روی مجموعهٔ ( TΣ ( N به صورت زیر تعرف می شود :
درخت ( t1∈ TΣ ( N می تواند در یک مرحله اشتقاق شود به درخت ( t1∈ TΣ ( N اگر وجود داشته باشد : متن S و انتقال A→t ) ∈ P ) به طوری که
• [t1 = S[A و
• [t2 = S[t.
در اینجا یک بافت ( متن ) به معنی یک درخت با دقیقاً یک حفره در آن است و [S[t نشان دهندهٔ نتیجهٔ پر کردن درخت T با حفره ای از S است .
زبان درخت تولید شده توسط T زبان { L ( G ) = { t ∈ TΣ | Z ⇒G* t است.
در اینجا TΣ نشان دهندهٔ مجموعه ای از تمام درختان تشکیل شده از نمادهای Σ , درحالیکه ⇒G* نشان دهندهٔ عملیات پی در پی از ⇒G است.
فرض کنید G1 = ( N1, Σ1 ) , Z1 , P1 که در آن
• {N1 = {Bool, BList مجموعه ای از غیرپایانه های ماست.
• {N1 = {Bool, BList الفبای رتبه بندی شدهٔ ماست که arities توسط استدلال های ساختگی نشان داده شده ( یعنی منفی نماد arity 2 است )
• Z1 = BList غیرپایانه آغازین است و
• مجموعهٔ P1 شامل موارد زیر می شود:
• Bool → false
• Bool → true
• BList → nil
• ( BList → cons ( Bool, BList
مثالی از اشتقاق گرامر G1 :
BList ⇒ cons ( Bool, BList ) ⇒ cons ( false, cons ( Bool, BList ) ) ⇒ cons ( false, cons ( true, nil ) )

wiki: گرامر درخت منظم
