در نظریه گراف گراف کنسر ( به انگلیسی: Kneser graph ) ، K G n , k ، گرافی است که رأس های آن نظیر زیرمجموعه های k عضوی از یک مجموعه ی n عضوی است. بین دو رأس یک یال وجود دارد اگر و تنها اگر زیرمجموعه های نظیر رأس ها ناسازگار باشند ( اشتراکشان تهی باشد ) . این گراف ها به نام مارتین کنسر نامگذاری شده اند که برای اولین بار آنها را در سال ۱۹۵۵ بررسی کرد.
• گراف کامل n رأسی گراف نسر K G n , 1 {\displaystyle KG_{n, 1}} است.
• گراف K G 5 , 2 {\displaystyle KG_{5, 2}} با گراف پترسن ایزومورف است.
• در گراف کنسر هر رأس با انتخاب k از n - k رأس دیگر مجاور است.
• همانگونه که کنسر حدس زد عدد رنگی گراف K G n , k {\displaystyle KG_{n, k}} دقیقاً برابر n - 2k+۲ است. لوواش در سال ۱۹۷۸ و جاشوآ در سال ۲۰۰۲ برای این فرمول اثبات هایی توپولوژیکی ارائه دادند. در سال ۲۰۰۴ ماتوشک اثباتی کاملاً ترکیبیاتی برای آن پیدا کرد.
• وقتی n بزرگتر مساوی ۳k باشد گراف کنسر همیشه دور هامیلتونی خواهد داشت ( چن ۲۰۰۰ ) . محاسبات نشان داده اند که همهٔ گراف های همبند کسزر با nهای کوچکتر مساوی ۲۷ به جز گراف پترسن، همیلتونی هستند.
• اگر n کوچکتر از ۳k باشد گراف کنسر هیچ مثلثی نخواهد داشت.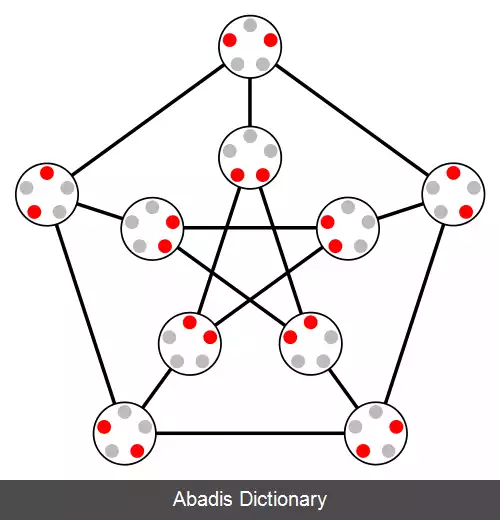
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلف• گراف کامل n رأسی گراف نسر K G n , 1 {\displaystyle KG_{n, 1}} است.
• گراف K G 5 , 2 {\displaystyle KG_{5, 2}} با گراف پترسن ایزومورف است.
• در گراف کنسر هر رأس با انتخاب k از n - k رأس دیگر مجاور است.
• همانگونه که کنسر حدس زد عدد رنگی گراف K G n , k {\displaystyle KG_{n, k}} دقیقاً برابر n - 2k+۲ است. لوواش در سال ۱۹۷۸ و جاشوآ در سال ۲۰۰۲ برای این فرمول اثبات هایی توپولوژیکی ارائه دادند. در سال ۲۰۰۴ ماتوشک اثباتی کاملاً ترکیبیاتی برای آن پیدا کرد.
• وقتی n بزرگتر مساوی ۳k باشد گراف کنسر همیشه دور هامیلتونی خواهد داشت ( چن ۲۰۰۰ ) . محاسبات نشان داده اند که همهٔ گراف های همبند کسزر با nهای کوچکتر مساوی ۲۷ به جز گراف پترسن، همیلتونی هستند.
• اگر n کوچکتر از ۳k باشد گراف کنسر هیچ مثلثی نخواهد داشت.

wiki: گراف کنسر
