گراف کامل

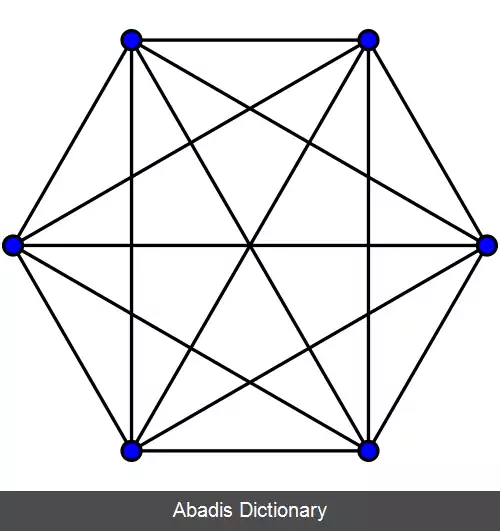
گراف کامل گراف ساده ای است که در آن هر رأس به تمامی راس های دیگر به وسیلهٔ یک یال متصل است. معمولاً گراف کاملِ n راسی را با k n نمایش میدهند. آغاز نظریه گراف ها معمولاً با کار اویلر بر روی هفت پلِ کونیکسبرگ در سال ۱۷۳۶ گره خورده است. [ ۱] با این حال، تاریخچه گرافهای کامل به رسم های رامون یوی در قرن سیزدهم بازمی گردد، که رئوس گراف را در گوشه های چندضلعی منتظم قرار میداد. [ ۲] [ ۳] این رسم ها با عنوان گل رز عرفانی نیز شناخته می شوند. [ ۴]
• تعداد یالهای یک گراف کامل n {\displaystyle n} راسی n × ( n − 1 ) 2 {\displaystyle {\frac {n\times {\bigl ( }n - 1{\bigr ) }}{2}}} است. [ ۵]
• هر گراف کاملی گروهک بیشین خود است. [ ۵]
• مکمل یک گراف کامل، گراف تهی است. [ ۵]
• تعداد تطابق های کامل یک گراف کامل n {\displaystyle n} راسی برابر است با ( n − 1 ) ! ! {\displaystyle ( n - 1 ) !!} . [ ۶]
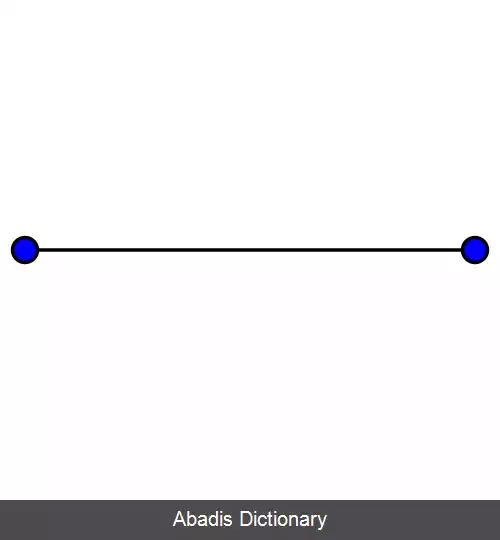
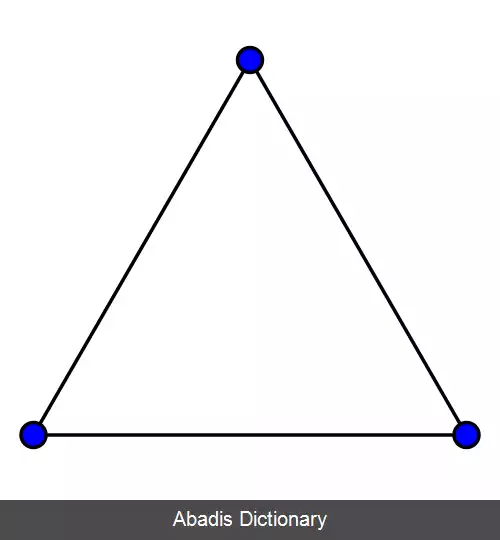
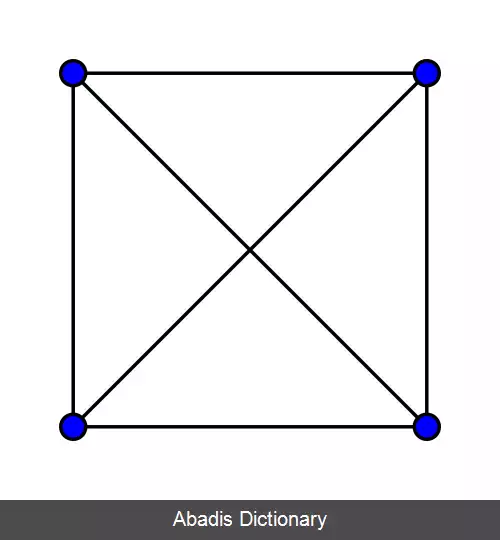
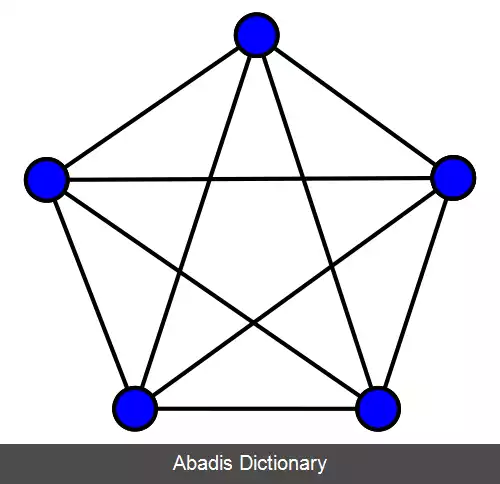
شکل پایین شامل گرافهای کامل که دارای یک تا هشت رأس هستند می باشد:
تمامی درایه های گراف کامل ۱ هستند به جز درایه های روی قطر اصلی که صفر هستند چون گراف کامل طوقه وجود ندارد.
n ∗ n