گراف کاتز یا K M N + 1 یک گراف جهت دار از مرتبهٔ M و بُعد N + 1 است که دارای ( M + 1 ) M N راس است که این راس ها به وسیلهٔ تمام رشته های ممکن s 0 ⋯ s N با طول N + 1 که از کارکترهای s i از الفبای A که شامل M + 1 نماد ( حرف ) مجزا است برچسب گذاری شده اند و در این برچسب گذاری هیچ دو حرف مجاوری برابر نیستند ( s i ≠ s i + 1 ) .
گراف کاتز K M N + 1 شامل ( M + 1 ) M N + 1 یال است
{ ( s 0 s 1 ⋯ s N , s 1 s 2 ⋯ s N s N + 1 ) | s i ∈ A s i ≠ s i + 1 }
معمول است که هر یال از K M N + 1 را با s 0 s 1 ⋯ s N + 1 برچسب گذاری می کنند، که این کار یک نگاشت دوسویی بین یال های گراف کاتز K M N + 1 و راس های گراف کاتز K M N + 2 را نتیجه می دهد.
کراف کاتز به طور بسیار نزدیکی به گراف دی براین مربوط است.
• برای یک درجهٔ ثابت M {\displaystyle M} و تعداد راس های V = ( M + 1 ) M N {\displaystyle V= ( M+1 ) M^{N}} ، گراف کاتز، کوچکترین فاصله را با هر گراف جهت دار ممکن با V {\displaystyle V} راس و M {\displaystyle M} یال دارد.
• همهٔ گراف های کاتز دارای دور اویلری هستند. ( دور اویلری دوری است که تمام یال ها را دقیقاً یک بار پیمایش می کند - - این نتیجه به این دلیل حاصل می شود که در گراف های کاتز درجهٔ ورودی هر راس با درجهٔ خروجی آن راس برابر است )
• تمام گراف های کاتز، دارای دور همیلتنی هستند. ( این نتیجه از نگاشت دوسویی که بین یال های گراف کاتز K M N {\displaystyle K_{M}^{N}} و راس های گراف کاتز K M N + 1 {\displaystyle K_{M}^{N+1}} تعریف شد حاصل می شود )
• یک گراف کاتز درجهٔ k {\displaystyle k} دارای k {\displaystyle k} مسیر مجزا از هر راس x {\displaystyle x} به راس دیگر y {\displaystyle y} است.
گراف کاتز به عنوان یک ساختار شبکه برای وصل کردن پردازشگرها در محاسبات بسیار سریع[ ۱] و محاسبات مقاوم در برابر خطا[ ۲] ، استفاده شده است. کاربرد: چنین شبکه هایی به عنوان شبکه کاتز شناخته می شوند.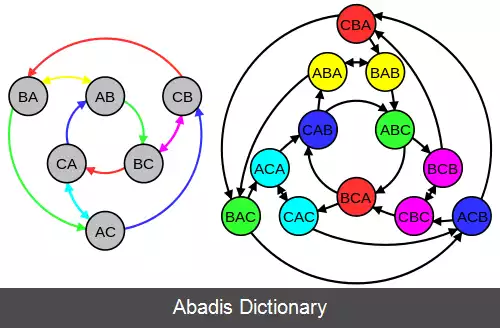
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفگراف کاتز K M N + 1 شامل ( M + 1 ) M N + 1 یال است
{ ( s 0 s 1 ⋯ s N , s 1 s 2 ⋯ s N s N + 1 ) | s i ∈ A s i ≠ s i + 1 }
معمول است که هر یال از K M N + 1 را با s 0 s 1 ⋯ s N + 1 برچسب گذاری می کنند، که این کار یک نگاشت دوسویی بین یال های گراف کاتز K M N + 1 و راس های گراف کاتز K M N + 2 را نتیجه می دهد.
کراف کاتز به طور بسیار نزدیکی به گراف دی براین مربوط است.
• برای یک درجهٔ ثابت M {\displaystyle M} و تعداد راس های V = ( M + 1 ) M N {\displaystyle V= ( M+1 ) M^{N}} ، گراف کاتز، کوچکترین فاصله را با هر گراف جهت دار ممکن با V {\displaystyle V} راس و M {\displaystyle M} یال دارد.
• همهٔ گراف های کاتز دارای دور اویلری هستند. ( دور اویلری دوری است که تمام یال ها را دقیقاً یک بار پیمایش می کند - - این نتیجه به این دلیل حاصل می شود که در گراف های کاتز درجهٔ ورودی هر راس با درجهٔ خروجی آن راس برابر است )
• تمام گراف های کاتز، دارای دور همیلتنی هستند. ( این نتیجه از نگاشت دوسویی که بین یال های گراف کاتز K M N {\displaystyle K_{M}^{N}} و راس های گراف کاتز K M N + 1 {\displaystyle K_{M}^{N+1}} تعریف شد حاصل می شود )
• یک گراف کاتز درجهٔ k {\displaystyle k} دارای k {\displaystyle k} مسیر مجزا از هر راس x {\displaystyle x} به راس دیگر y {\displaystyle y} است.
گراف کاتز به عنوان یک ساختار شبکه برای وصل کردن پردازشگرها در محاسبات بسیار سریع[ ۱] و محاسبات مقاوم در برابر خطا[ ۲] ، استفاده شده است. کاربرد: چنین شبکه هایی به عنوان شبکه کاتز شناخته می شوند.

wiki: گراف کاتز
