گراف مکمل
فرهنگستان زبان و ادب
دانشنامه عمومی
در نظریه گراف، مکمّل یا معکوس گراف G، گراف H با رئوس یکسان است به طوری که دو رأس متمایز H مجاورند اگر و فقط اگر آن دو راس در G مجاور نباشند. به این معنا که برای تولید مکمل یک گراف، تمام یال های غایب مورد نیاز برای تشکیل یک گراف کامل اضافه می شوند و تمام یال هایی که قبلاً وجود داشتند حذف می گردند. [ ۱]
فرض کنید G = ( V, E ) یک گراف ساده باشد و K مجموعهٔ تمام زیرمجموعه های ۲ - عضوی V است. در این صورت، H = ( V, K \ E ) گرافِ مکمّلِ گرافِ Gست، [ ۲] که در آن K \ E متمم نسبی E در K است. برای گراف های جهت دار، می توان مکمَل را به همین شکل تعریف کرد؛ یعنی به عنوان یک گراف جهت دار با مجموعه رئوس یک سان با استفاده از مجموعهٔ تمام زوج مرتب های ۲ - عضوی از V به عنوان K در عبارت مذکور.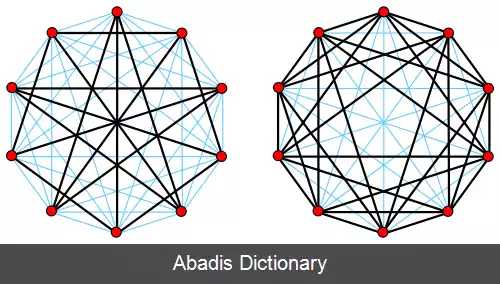
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلففرض کنید G = ( V, E ) یک گراف ساده باشد و K مجموعهٔ تمام زیرمجموعه های ۲ - عضوی V است. در این صورت، H = ( V, K \ E ) گرافِ مکمّلِ گرافِ Gست، [ ۲] که در آن K \ E متمم نسبی E در K است. برای گراف های جهت دار، می توان مکمَل را به همین شکل تعریف کرد؛ یعنی به عنوان یک گراف جهت دار با مجموعه رئوس یک سان با استفاده از مجموعهٔ تمام زوج مرتب های ۲ - عضوی از V به عنوان K در عبارت مذکور.

wiki: گراف مکمل
پیشنهاد کاربران
پیشنهادی ثبت نشده است. شما اولین نفر باشید
