در نظریه گراف ها، گراف مسطح گرافی است که می تواند در یک صفحه محاط شود. برای مثال یک گراف مسطح را می توان به گونه ای رسم کرد که یال هایش یکدیگر را تنها در رأس ها قطع کنند.
یک گراف غیرمسطح گرافی است که نمی توان آن را به گونه ای رسم کرد که یال هایش یکدیگر را در نقاطی غیراز رأس ها قطع نکنند.
گراف مسطحی که بدون تقاطع یال ها در صفحه ترسیم شده باشد را صفحه گراف یا گراف محاط در صفحه می نامند. یک صفحه گراف را می توان به صورت یک گراف مسطح تعریف کرد که هر گره ای را به نقطه ای در فضای دوبعدی و هر یالی را به خمی در صفحه می نگارد به گونه ای که نقاط انتهایی هر خم نقاطی هستند که از گره ها نگاشته شده اند، و خم ها هیچ اشتراکی با یکدیگر ندارند مگر در نقاط انتهایی.
به سادگی دیده می شود که گرافی که قابل ترسیم در صفحه است را می توان در کره نیز ترسیم کرد.
ریاضی دان لهستانی کازیمیر کوراتوسکی ( به انگلیسی: Kazimierz Kuratowski ) توصیفی از گراف های مسطح را تحت عنوان گراف های ممنوعه ارائه کرده است، که امروزه تحت عنوان نظریه کوراتوسکی شناخته می شود.
یک گراف متناهی مسطح است، اگر و تنها اگر شامل زیرگرافی نباشد که آن زیرگراف، زیربخشی از گراف K5 ( گراف کامل با ۵ رأس ) یا K3, 3 ( گراف کامل دوبخشی با ۶ رأس که ۳ رأس از آن در یک طرف به ۳ رأس دیگر در طرف مقابل متصل اند ) باشد.
یک زیربخش از یک گراف نتیجه قراردادن رئوسی در میان یال هاست ( برای مثال یال •——• به یال •—•—• تغییر یابد. ) بدین ترتیب که این روند صفر مرتبه یا بیشتر تکرار شود. قواعد معادل این نظریه که تحت عنوان "نظریهٔ P" نیز شناخته می شوند می گویند: یک گراف متناهی مسطح است اگر و تنها اگر شامل زیرگرافی هم ریخت با K5 یا K3, 3 نباشند.
در شوروی نظریه کوراتوسکی تحت عنوان نظریهٔ Pontryagin - Kuratowski شناخته می شود. زیرا گفته می شود که اثبات آن نخستین بار در دست نوشته های منتشر نشده Pontryagin بوده است. بنابر فهم های رایج آکادمیک چنین منابعی در اولویت قرار ندارند. از این رو نام روسی این نظریه به طور بین المللی مورد تأیید نیست.
به جای در نظر گرفتن زیربخش ها نظریهٔ واگنر با کهادها سر و کار دارد:
یک گراف مسطح است، اگر و تنها اگر دارای K5 یا K3, 3 به عنوان کهاد نباشد.
واگنر به طور عمومی تری بیان کرد که هر دسته ای از بسته های کهاد با مجموعه ای محدود از کهادهای ممنوعه مشخص می شوند. این مسئله امروزه نظریه Robertson - Seymour نامیده می شود، که در صفحات فراوانی این نظریه به اثبات رسیده است. در ادبیات این نظریه K5 و K3, 3 فرزندان ممنوعه ای برای دستهٔ گراف های مسطح متناهی هستند.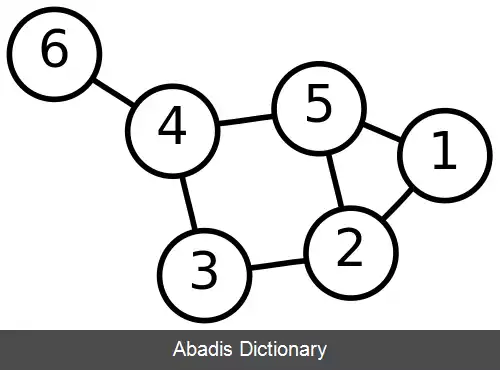
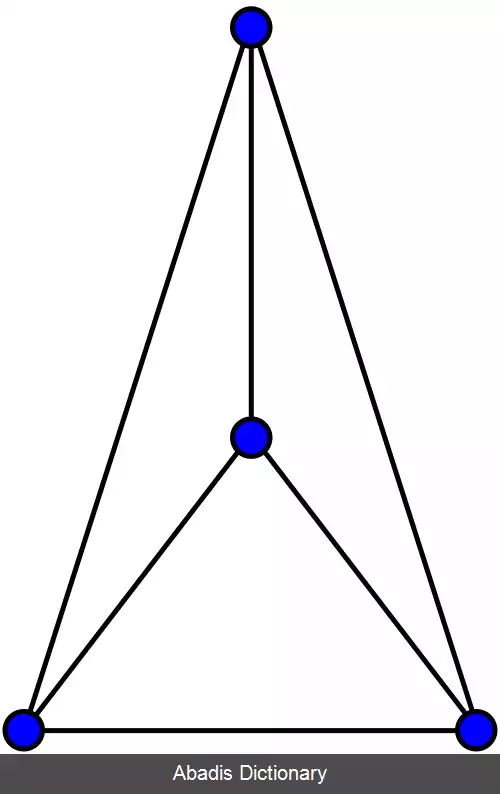
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک گراف غیرمسطح گرافی است که نمی توان آن را به گونه ای رسم کرد که یال هایش یکدیگر را در نقاطی غیراز رأس ها قطع نکنند.
گراف مسطحی که بدون تقاطع یال ها در صفحه ترسیم شده باشد را صفحه گراف یا گراف محاط در صفحه می نامند. یک صفحه گراف را می توان به صورت یک گراف مسطح تعریف کرد که هر گره ای را به نقطه ای در فضای دوبعدی و هر یالی را به خمی در صفحه می نگارد به گونه ای که نقاط انتهایی هر خم نقاطی هستند که از گره ها نگاشته شده اند، و خم ها هیچ اشتراکی با یکدیگر ندارند مگر در نقاط انتهایی.
به سادگی دیده می شود که گرافی که قابل ترسیم در صفحه است را می توان در کره نیز ترسیم کرد.
ریاضی دان لهستانی کازیمیر کوراتوسکی ( به انگلیسی: Kazimierz Kuratowski ) توصیفی از گراف های مسطح را تحت عنوان گراف های ممنوعه ارائه کرده است، که امروزه تحت عنوان نظریه کوراتوسکی شناخته می شود.
یک گراف متناهی مسطح است، اگر و تنها اگر شامل زیرگرافی نباشد که آن زیرگراف، زیربخشی از گراف K5 ( گراف کامل با ۵ رأس ) یا K3, 3 ( گراف کامل دوبخشی با ۶ رأس که ۳ رأس از آن در یک طرف به ۳ رأس دیگر در طرف مقابل متصل اند ) باشد.
یک زیربخش از یک گراف نتیجه قراردادن رئوسی در میان یال هاست ( برای مثال یال •——• به یال •—•—• تغییر یابد. ) بدین ترتیب که این روند صفر مرتبه یا بیشتر تکرار شود. قواعد معادل این نظریه که تحت عنوان "نظریهٔ P" نیز شناخته می شوند می گویند: یک گراف متناهی مسطح است اگر و تنها اگر شامل زیرگرافی هم ریخت با K5 یا K3, 3 نباشند.
در شوروی نظریه کوراتوسکی تحت عنوان نظریهٔ Pontryagin - Kuratowski شناخته می شود. زیرا گفته می شود که اثبات آن نخستین بار در دست نوشته های منتشر نشده Pontryagin بوده است. بنابر فهم های رایج آکادمیک چنین منابعی در اولویت قرار ندارند. از این رو نام روسی این نظریه به طور بین المللی مورد تأیید نیست.
به جای در نظر گرفتن زیربخش ها نظریهٔ واگنر با کهادها سر و کار دارد:
یک گراف مسطح است، اگر و تنها اگر دارای K5 یا K3, 3 به عنوان کهاد نباشد.
واگنر به طور عمومی تری بیان کرد که هر دسته ای از بسته های کهاد با مجموعه ای محدود از کهادهای ممنوعه مشخص می شوند. این مسئله امروزه نظریه Robertson - Seymour نامیده می شود، که در صفحات فراوانی این نظریه به اثبات رسیده است. در ادبیات این نظریه K5 و K3, 3 فرزندان ممنوعه ای برای دستهٔ گراف های مسطح متناهی هستند.


wiki: گراف مسطح
