گراف فراخوانی ( که به عنوان مولتی گراف فراخوانی[ ۱] نیز شناخته می شود ) یک گراف کنترل جریان است، که روابط فراخوانی بین زیر برنامه ها را در یک برنامه کامپیوتری نشان می دهد. هر راس یک دستور العمل را نشان می دهد و هر یال ( f, g ) نشان می دهد که دستورالعمل f روند g را فراخوانی می کند. در نتیجه، یک چرخه در گراف فراخوانی رویه بازگشتی را نشان می دهد.
گراف های فراخوانی می توانند پویا یا ایستا باشند. [ ۲] یک گراف فراخوانی پویا یک ثبت از اجرای برنامه است، به عنوان مثال به عنوان خروجی توسط یک پروفایلر؛ بنابراین، یک گراف فراخوانی پویا می تواند دقیق باشد، اما فقط یک بار اجرای برنامه را توصیف می کند. یک گراف فراخوانی ایستا یک گراف فراخوانی است که طراحی شده است تا همهٔ اجراهای ممکن برنامه را نمایش دهد. داشتن گراف فراخوانی استاتیک کاملاً دقیق یک مسئله حل نشدنی است، بنابراین الگوریتم های گراف فراخوانی استاتیک معمولاً با تقریب بیش از حد به دست آمده اند؛ یعنی هر رابطه فراخوانی که رخ می دهد در گراف نشان داده می شود، و احتمالاً برخی از روابط فراخوانی که هرگز در اجرای واقعی برنامه رخ نمی دهند نیز در گراف نمایش داده می شوند.
گرافهای فراخوانی را می توان طوری تعریف کرد که بتوانند درجات مختلفی از دقت را نمایش دهند. یک گراف فراخوانی دقیق تر، رفتار برنامه واقعی را با دقت بیشتری تقریب می کند، به قیمت اینکه زمان بیشتری برای محاسبه کردن و حافظه بیشتری برای ذخیره سازی نیاز داریم. دقیق ترین گراف فراخوانی کاملاً به متن حساس است، به این معنی که گراف برای هر دستور العمل، شامل یک راس جداگانه برای هر پشته فراخوانی است که می توان با آن دستور العمل را فعال کرد. یک گراف فراخوانی کاملاً حساس به متن، درخت فراخوانی محتوا نامیده می شود. این را می توان به راحتی به صورت پویا محاسبه کرد، اگرچه ممکن است مقدار زیادی از حافظه را اشغال کند. فراخوانی درخت های محتوا معمولاً به صورت ایستا محاسبه نمی شود، زیرا ممکن است برای یک برنامه بزرگ خیلی زمان بر باشد. گراف فراخوانی این که کمترین دقت را دارد گراف فراخوانی غیر حساس به متن است، به این معنی که برای هر رویه فقط یک راس وجود دارد.
با زبان هایی که دارای ارسال پویا هستند، مانند جاوا و C++، محاسبه یک گراف فراخوانی ایستا دقیقاً به نتایج تجزیه و تحلیل مستعار نیاز دارد. [ ۳] و برعکس، محاسبه نام مستعار دقیق به یک گراف فراخوانی نیاز دارد. بسیاری از سیستم های تجزیه و تحلیل استاتیک، رگرسیون نامتناهی ظاهری را با محاسبه آن دو به طور همزمان حل می کنند.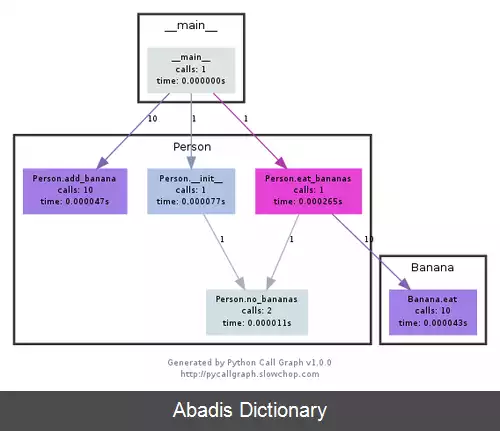
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفگراف های فراخوانی می توانند پویا یا ایستا باشند. [ ۲] یک گراف فراخوانی پویا یک ثبت از اجرای برنامه است، به عنوان مثال به عنوان خروجی توسط یک پروفایلر؛ بنابراین، یک گراف فراخوانی پویا می تواند دقیق باشد، اما فقط یک بار اجرای برنامه را توصیف می کند. یک گراف فراخوانی ایستا یک گراف فراخوانی است که طراحی شده است تا همهٔ اجراهای ممکن برنامه را نمایش دهد. داشتن گراف فراخوانی استاتیک کاملاً دقیق یک مسئله حل نشدنی است، بنابراین الگوریتم های گراف فراخوانی استاتیک معمولاً با تقریب بیش از حد به دست آمده اند؛ یعنی هر رابطه فراخوانی که رخ می دهد در گراف نشان داده می شود، و احتمالاً برخی از روابط فراخوانی که هرگز در اجرای واقعی برنامه رخ نمی دهند نیز در گراف نمایش داده می شوند.
گرافهای فراخوانی را می توان طوری تعریف کرد که بتوانند درجات مختلفی از دقت را نمایش دهند. یک گراف فراخوانی دقیق تر، رفتار برنامه واقعی را با دقت بیشتری تقریب می کند، به قیمت اینکه زمان بیشتری برای محاسبه کردن و حافظه بیشتری برای ذخیره سازی نیاز داریم. دقیق ترین گراف فراخوانی کاملاً به متن حساس است، به این معنی که گراف برای هر دستور العمل، شامل یک راس جداگانه برای هر پشته فراخوانی است که می توان با آن دستور العمل را فعال کرد. یک گراف فراخوانی کاملاً حساس به متن، درخت فراخوانی محتوا نامیده می شود. این را می توان به راحتی به صورت پویا محاسبه کرد، اگرچه ممکن است مقدار زیادی از حافظه را اشغال کند. فراخوانی درخت های محتوا معمولاً به صورت ایستا محاسبه نمی شود، زیرا ممکن است برای یک برنامه بزرگ خیلی زمان بر باشد. گراف فراخوانی این که کمترین دقت را دارد گراف فراخوانی غیر حساس به متن است، به این معنی که برای هر رویه فقط یک راس وجود دارد.
با زبان هایی که دارای ارسال پویا هستند، مانند جاوا و C++، محاسبه یک گراف فراخوانی ایستا دقیقاً به نتایج تجزیه و تحلیل مستعار نیاز دارد. [ ۳] و برعکس، محاسبه نام مستعار دقیق به یک گراف فراخوانی نیاز دارد. بسیاری از سیستم های تجزیه و تحلیل استاتیک، رگرسیون نامتناهی ظاهری را با محاسبه آن دو به طور همزمان حل می کنند.

wiki: گراف فراخوانی
