در نظریه گراف ها، یک مبحث ریاضی، گراف فاکتور بحرانی یا گراف هایپومچبل ( به انگلیسی: Factor - critical graph ) یک گراف با n راس می باشد به طوری که هر زیر گراف n - 1 عضوی دارای خاصیت تطابق کامل می باشد. ( تطابق کامل در یک گراف به این معنی است که یک زیر مجموعه از یال های این گراف هستند که در این زیر مجموعه هر یک از راس ها دقیقاً نقطه پایانی یکی از یال ها هستند.
نوع دیگری از اتصال که در آن تمامی راس ها به جز یکی از آن ها پوشش داده می شوند تطابق کامل نزدیک ( near - perfect matching ) نامیده می شود. پس به طور مشابه یک گراف فاکتور_بحرانی گرافی است که در آن تطابق های کامل نزدیک وجود داشته باشد طوری که در هر کدام از یکی از راس ها صرف نظر شده باشد.
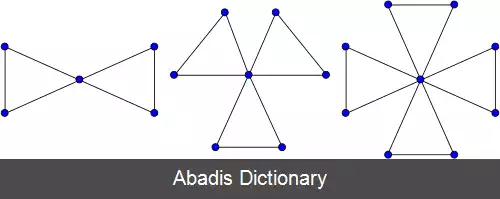
هر دور به طول فرد یک گراف فاکتور_بحرانی می باشد، همانطور که هر گراف کامل با تعداد فرد راس یک گراف فاکتور_بحرانی می باشد. به طور عمومی هر گراف همیلتونی با تعداد فرد راس یک گراف فاکتور_بحرانی می باشد. گراف های دوستی یا friendship graphs ( گراف هایی که از اتصال مجموعه ای از مثلث ها به وجود آمده و در یک راس مشترک هستند ) مثال دیگری از گراف فاکتور_بحرانی ها هستند با این تفاوت که این گراف ها غیر همیلتونی هستند. هر گراف همبند پنجه آزاد ( claw - free ) با تعداد فرد راس، یک گراف فاکتور_بحرانی می باشد. برای مثال گراف ۱۱ راسی که از حذف یک راس از بیست وجهی منتظم به وجود می آید و همبند نیز می باشد، یک گراف فاکتور_بحرانی می باشد. این نتیجه به طور مستقیم از یک قضیه بنیادی تر با این مضمون که هر گراف پنجه آزادِ همبند که دارای تعدادی زوج راس باشد حتماً دارای یک تطابق کامل می باشد، حاصل می شود.
گراف های فاکتور - بحرانی را می توان با چندین راه مختلف توصیف و تشریح کرد، جدا از تعریف آن ها به عنوان گراف هایی که در آن ها با حذف یک راس می توان یک تطابق کامل ایجاد کرد، تعاریف و ویژگی های دیگری نیز دارند به این صورت که:
Tibor Gallai ثابت کرد که گرافی می تواند فاکتور - بحرانی باشد اگر و تنها اگر همبند باشد و به ازای هر راس v از گراف، یک تطابق حداکثری وجود داشته باشد طوری که شامل راس v نشود. این نتیجه از این ویژگی که گراف باید دارای تعدادی فرد راس بوده طوری که هر تطابق حداکثر باید همه راس ها به جز یکی را به هم مرتبط کند، استنتاج می شود.
لاسلو لوواس نیز ثابت کرد که گرافی فاکتور بحرانی می باشد اگر و تنها اگر تعدادی فرد تجزیه گوشی داشته باشد ( یک دسته بندی از یال های گراف به دنباله ای از زیرگراف ها گفته می شود به طوری که هر یک از این زیرگراف های دارای دور یا مسیری به طول فرد باشند، به این ترتیب که اولین زیرگراف یک دور باشد و بعد از آن زیرگراف ها هرکدام مسیری باشند که دارای نقطه های پایانی هستند و هر راس داخلی نباید در زیرگراف قبلی وجود داشته باشد، همچنین هر دور به غیر از دور اول در دنباله دقیقاً یک راس در زیرگراف های قبلی داشته باشد. برای مثال گراف نمایش داده شده در شکل ممکن است با این روش به یک دور با ۵ یال و یک مسیر با ۳ یال تقسیم بندی شود. در مواردی که تطابق کامل نزدیک برای گراف فاکتور بحرانی داده شود، دسته های جدا شدنی می توانند به نحوی انتخاب شوند که دسته های جدا شدنی بین یال های تطبیق یافته و تطبیق نیافته متبادل شوند.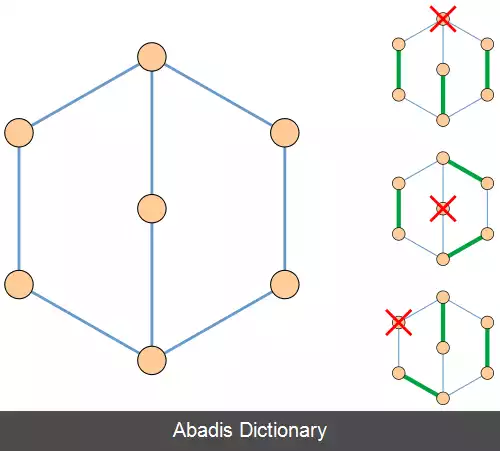
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفنوع دیگری از اتصال که در آن تمامی راس ها به جز یکی از آن ها پوشش داده می شوند تطابق کامل نزدیک ( near - perfect matching ) نامیده می شود. پس به طور مشابه یک گراف فاکتور_بحرانی گرافی است که در آن تطابق های کامل نزدیک وجود داشته باشد طوری که در هر کدام از یکی از راس ها صرف نظر شده باشد.
هر دور به طول فرد یک گراف فاکتور_بحرانی می باشد، همانطور که هر گراف کامل با تعداد فرد راس یک گراف فاکتور_بحرانی می باشد. به طور عمومی هر گراف همیلتونی با تعداد فرد راس یک گراف فاکتور_بحرانی می باشد. گراف های دوستی یا friendship graphs ( گراف هایی که از اتصال مجموعه ای از مثلث ها به وجود آمده و در یک راس مشترک هستند ) مثال دیگری از گراف فاکتور_بحرانی ها هستند با این تفاوت که این گراف ها غیر همیلتونی هستند. هر گراف همبند پنجه آزاد ( claw - free ) با تعداد فرد راس، یک گراف فاکتور_بحرانی می باشد. برای مثال گراف ۱۱ راسی که از حذف یک راس از بیست وجهی منتظم به وجود می آید و همبند نیز می باشد، یک گراف فاکتور_بحرانی می باشد. این نتیجه به طور مستقیم از یک قضیه بنیادی تر با این مضمون که هر گراف پنجه آزادِ همبند که دارای تعدادی زوج راس باشد حتماً دارای یک تطابق کامل می باشد، حاصل می شود.
گراف های فاکتور - بحرانی را می توان با چندین راه مختلف توصیف و تشریح کرد، جدا از تعریف آن ها به عنوان گراف هایی که در آن ها با حذف یک راس می توان یک تطابق کامل ایجاد کرد، تعاریف و ویژگی های دیگری نیز دارند به این صورت که:
Tibor Gallai ثابت کرد که گرافی می تواند فاکتور - بحرانی باشد اگر و تنها اگر همبند باشد و به ازای هر راس v از گراف، یک تطابق حداکثری وجود داشته باشد طوری که شامل راس v نشود. این نتیجه از این ویژگی که گراف باید دارای تعدادی فرد راس بوده طوری که هر تطابق حداکثر باید همه راس ها به جز یکی را به هم مرتبط کند، استنتاج می شود.
لاسلو لوواس نیز ثابت کرد که گرافی فاکتور بحرانی می باشد اگر و تنها اگر تعدادی فرد تجزیه گوشی داشته باشد ( یک دسته بندی از یال های گراف به دنباله ای از زیرگراف ها گفته می شود به طوری که هر یک از این زیرگراف های دارای دور یا مسیری به طول فرد باشند، به این ترتیب که اولین زیرگراف یک دور باشد و بعد از آن زیرگراف ها هرکدام مسیری باشند که دارای نقطه های پایانی هستند و هر راس داخلی نباید در زیرگراف قبلی وجود داشته باشد، همچنین هر دور به غیر از دور اول در دنباله دقیقاً یک راس در زیرگراف های قبلی داشته باشد. برای مثال گراف نمایش داده شده در شکل ممکن است با این روش به یک دور با ۵ یال و یک مسیر با ۳ یال تقسیم بندی شود. در مواردی که تطابق کامل نزدیک برای گراف فاکتور بحرانی داده شود، دسته های جدا شدنی می توانند به نحوی انتخاب شوند که دسته های جدا شدنی بین یال های تطبیق یافته و تطبیق نیافته متبادل شوند.



wiki: گراف فاکتور بحرانی
