در نظریه گراف، یک گراف دی بروین n بعدی از m نماد، یک گراف جهت دار است که روی هم افتادگی توالی های نمادها را نشان می دهد. این گراف m n راس دارد و شامل تمام توالی های ممکن به طول n از نمادهای داده شده است. یک نماد ممکن است چندین بار در یک توالی ظاهر شود. اگر یک مجموعه از m نماد داشته باشیم، یعنی S := { s 1 , … , s m } ، آنگاه مجموعهٔ راس ها عبارت است از:
اگر یکی از راس ها بتواند به وسیلهٔ شیفت دادن نمادهای راسی دیگر به اندازهٔ یک مکان به چپ و اضافه کردن یک نماد جدید به انتهای آن بیان شود، آنگاه راس دوم یک یال جهت دار به راس اول خواهد داشت. به عبارت دیگر اگر پسوند راس دوم ( شامل n − 1 نماد ) برابر پیشوند راس اول ( شامل n − 1 نماد ) شود، آنگاه یک یال جهت دار از راس دوم به راس اول وجود خواهد داشت. بنابراین مجموعهٔ یال ها ( جهت دار ) عبارت است از:
اگرچه گراف های دی بروین به نام نیکولا گواروت دی برویان نامگذاری شده است، اما این گرافها به طور مستقل توسط دی برویان[ ۱] و آی جی گود[ ۲] کشف شده اند. البته پیش از این کامیل فلای سینت ماری به صورت ضمنی از خواص این گراف ها استفاده کرده بود. [ ۳]
• اگر n = 1 {\displaystyle n=1} باشد، آنگاه شرایط گفته شده برای هر دو راسی که باید تشکیل یال بدهند، بی معنی خواهد بود و تمام راس ها به وسیلهٔ m 2 {\displaystyle m^{2}} یال به هم متصل خواهند بود.
• هر راس دقیقاً m {\displaystyle m} یال ورودی و m {\displaystyle m} یال خروجی خواهد داشت.
• هر گراف n {\displaystyle n} بعدی دی بروین، یک گراف جهت دار خطی از گراف دی بر این n − 1 {\displaystyle n - 1} بعدی با همان مجموعه نمادها است.
• هر گراف دی بروین گراف اویلری یا گراف همیلتونی است. دور اویلری و دور همیلتونی در این گراف ها توالی دی بروین را نشان می دهند.
ساختار گراف خطی از ۳ تا از کوچکترین گراف دی بر این دودویی در شکل زیر نمایش داده شده است. همان طور که مشاهده می شود، هر راس از گراف دی بر این n بعدی، نشان دهندهٔ یک یال از گراف دی بر این n − 1 بعدی است.
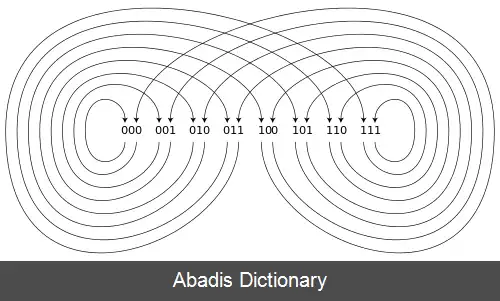
گراف های دی بروین دودویی می توانند به طریقی رسم شود که شبیه اشیاء نظریهٔ سیستم های دینامیکی باشند، مانند مجذوب کننده ی لورنز:
• دنباله دبروین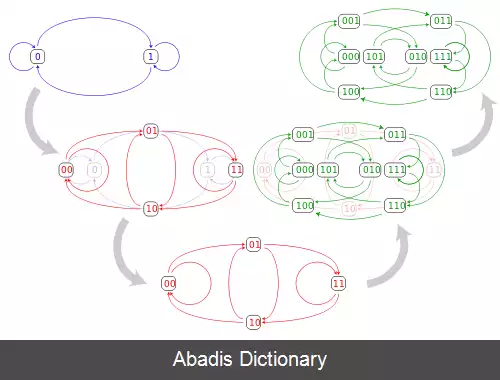

این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاگر یکی از راس ها بتواند به وسیلهٔ شیفت دادن نمادهای راسی دیگر به اندازهٔ یک مکان به چپ و اضافه کردن یک نماد جدید به انتهای آن بیان شود، آنگاه راس دوم یک یال جهت دار به راس اول خواهد داشت. به عبارت دیگر اگر پسوند راس دوم ( شامل n − 1 نماد ) برابر پیشوند راس اول ( شامل n − 1 نماد ) شود، آنگاه یک یال جهت دار از راس دوم به راس اول وجود خواهد داشت. بنابراین مجموعهٔ یال ها ( جهت دار ) عبارت است از:
اگرچه گراف های دی بروین به نام نیکولا گواروت دی برویان نامگذاری شده است، اما این گرافها به طور مستقل توسط دی برویان[ ۱] و آی جی گود[ ۲] کشف شده اند. البته پیش از این کامیل فلای سینت ماری به صورت ضمنی از خواص این گراف ها استفاده کرده بود. [ ۳]
• اگر n = 1 {\displaystyle n=1} باشد، آنگاه شرایط گفته شده برای هر دو راسی که باید تشکیل یال بدهند، بی معنی خواهد بود و تمام راس ها به وسیلهٔ m 2 {\displaystyle m^{2}} یال به هم متصل خواهند بود.
• هر راس دقیقاً m {\displaystyle m} یال ورودی و m {\displaystyle m} یال خروجی خواهد داشت.
• هر گراف n {\displaystyle n} بعدی دی بروین، یک گراف جهت دار خطی از گراف دی بر این n − 1 {\displaystyle n - 1} بعدی با همان مجموعه نمادها است.
• هر گراف دی بروین گراف اویلری یا گراف همیلتونی است. دور اویلری و دور همیلتونی در این گراف ها توالی دی بروین را نشان می دهند.
ساختار گراف خطی از ۳ تا از کوچکترین گراف دی بر این دودویی در شکل زیر نمایش داده شده است. همان طور که مشاهده می شود، هر راس از گراف دی بر این n بعدی، نشان دهندهٔ یک یال از گراف دی بر این n − 1 بعدی است.
گراف های دی بروین دودویی می توانند به طریقی رسم شود که شبیه اشیاء نظریهٔ سیستم های دینامیکی باشند، مانند مجذوب کننده ی لورنز:
• دنباله دبروین



wiki: گراف دی براین
