یک شبکه ارتباطی در برابر نقص دارای قدرت تحمل است اگر دارای مسیرهای دیگری میان راس ها باشد. هر چه مسیرهای مجزا بیشتر باشد٫ بهتر است. این مثال دقیقا مفهوم گراف چند همبند ( به انگلیسی: k - vertex - connected graph ) است.
گراف دوهمبند ( به انگلیسی: biconnected ) حالت خاصی از گراف چند همبند است.
گراف دوهمبند٫ یک گراف همبند است با این خصوصیت که غیر جداشدنی باشد٫ یعنی با حذف یک راس همبند باقی بماند. این خاصیت برای مدیریت یک گراف با افزونگی دوگانه[ ۱] سودمند است به این منظور که از ناهمبند شدن گراف با حذف یک یال آن جلوگیری شود.
به جهت خاصیت افزونگی٫ استفاده از گراف دوهمبند در زمینه شبکه ( ببینید شبکه شاره[ ۲] ) ٫ بسیار مهم است.
قضیه. ( ویتنی[ ۳] ) یک گراف بیسوی G که دارای حداقل سه راس باشد٫ دوهمبند است اگر٫ و فقط اگر٫ هر جفت u , v ∈ V ( G ) به وسیلهٔ دو مسیر درونی مجزا٫ یعنی مسیری که به غیر از u و v راس مشترک دیگری ندارد٫ به هم وصل شوند.
اگر G یک گراف k - همبند باشد و G ′ از G با افزودن یک راس جدید y مجاور با حداقل k راس از G٫ یه دست آید٫ آن گاه G ′ k - همبند است.
قضیه. اگر ۳ n ( G ) ≥ ٫ آن گاه شرایط زیر برای گراف های دوهمبند برقرار و هم ارز هستند.
الف ) G همبند است و دارای هیج راس برشی نیست.
ب ) به ازای هر x , y ∈ V ( G ) مسیرهای درونی مجزا وجود دارد.
پ ) به ازای هر x , y ∈ V ( G ) یک دور میان x و y وجود دارد.
ت ) ۱ δ ( G ) ≥ ٫ و هر جفت از یال ها در ٫G روی یک دور مشترک قرار می گیرند.
زیرتقسیم یال u v از یک گراف بیسوی G عبارت است از حذف u v و افزودن مسیر جدید u , w , v میان یک راس جدید w .
فرع. اگر G دوهمبند باشد٫ آن گاه گراف G ′ به دست آمده از زیر تقسیم یک یال ٫G دوهمبند است.
یک مسیر افزودن به ٫G افزودن مسیری است به G با طول ۱ l ≥ میان دو راس از G ٫ که l − 1 راس جدید را ارایٔه می کند. مسیر افزوده شده را دسته می گویند.
یک تجزیه دسته عبارت است از افراز E ( G ) به مجموعه های P 0 , P 1 , . . . , P k به طوری که P 0 یک دور باشد٫ و P i به ازای ۱ i ≥ یک مسیر افزودن به گراف تشکیل شده به وسیلهٔ P 0 , P 1 , . . . , P i − 1 باشد.
قضیه. ( ویتنی ) . یک گراف دو همبند است اگر٫ و فقط اگر٫ دارای یک تجزیه دسته باشد. علاوه بر این٫ هر دور در یک گراف دوهمبند٫ دور آغازی در یک تجزیه دسته است.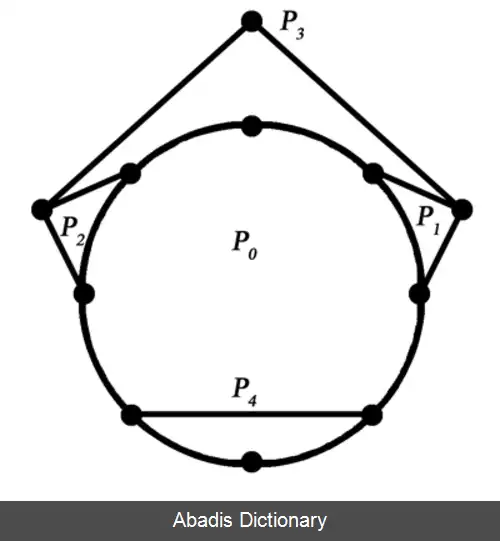
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفگراف دوهمبند ( به انگلیسی: biconnected ) حالت خاصی از گراف چند همبند است.
گراف دوهمبند٫ یک گراف همبند است با این خصوصیت که غیر جداشدنی باشد٫ یعنی با حذف یک راس همبند باقی بماند. این خاصیت برای مدیریت یک گراف با افزونگی دوگانه[ ۱] سودمند است به این منظور که از ناهمبند شدن گراف با حذف یک یال آن جلوگیری شود.
به جهت خاصیت افزونگی٫ استفاده از گراف دوهمبند در زمینه شبکه ( ببینید شبکه شاره[ ۲] ) ٫ بسیار مهم است.
قضیه. ( ویتنی[ ۳] ) یک گراف بیسوی G که دارای حداقل سه راس باشد٫ دوهمبند است اگر٫ و فقط اگر٫ هر جفت u , v ∈ V ( G ) به وسیلهٔ دو مسیر درونی مجزا٫ یعنی مسیری که به غیر از u و v راس مشترک دیگری ندارد٫ به هم وصل شوند.
اگر G یک گراف k - همبند باشد و G ′ از G با افزودن یک راس جدید y مجاور با حداقل k راس از G٫ یه دست آید٫ آن گاه G ′ k - همبند است.
قضیه. اگر ۳ n ( G ) ≥ ٫ آن گاه شرایط زیر برای گراف های دوهمبند برقرار و هم ارز هستند.
الف ) G همبند است و دارای هیج راس برشی نیست.
ب ) به ازای هر x , y ∈ V ( G ) مسیرهای درونی مجزا وجود دارد.
پ ) به ازای هر x , y ∈ V ( G ) یک دور میان x و y وجود دارد.
ت ) ۱ δ ( G ) ≥ ٫ و هر جفت از یال ها در ٫G روی یک دور مشترک قرار می گیرند.
زیرتقسیم یال u v از یک گراف بیسوی G عبارت است از حذف u v و افزودن مسیر جدید u , w , v میان یک راس جدید w .
فرع. اگر G دوهمبند باشد٫ آن گاه گراف G ′ به دست آمده از زیر تقسیم یک یال ٫G دوهمبند است.
یک مسیر افزودن به ٫G افزودن مسیری است به G با طول ۱ l ≥ میان دو راس از G ٫ که l − 1 راس جدید را ارایٔه می کند. مسیر افزوده شده را دسته می گویند.
یک تجزیه دسته عبارت است از افراز E ( G ) به مجموعه های P 0 , P 1 , . . . , P k به طوری که P 0 یک دور باشد٫ و P i به ازای ۱ i ≥ یک مسیر افزودن به گراف تشکیل شده به وسیلهٔ P 0 , P 1 , . . . , P i − 1 باشد.
قضیه. ( ویتنی ) . یک گراف دو همبند است اگر٫ و فقط اگر٫ دارای یک تجزیه دسته باشد. علاوه بر این٫ هر دور در یک گراف دوهمبند٫ دور آغازی در یک تجزیه دسته است.

wiki: گراف دوهمبند
