گراف دوبخشی
فرهنگستان زبان و ادب
دانشنامه عمومی
در نظریهٔ گراف ( یکی از شاخه های ریاضیات ) ، گراف دوبخشی گرافی است که راس هایش را می توان به دو مجموعهٔ مجزا مثل U و V تقسیم کرد، طوری که هر یال از آن گراف، یک راس از U را به یک راس از V متصل می کند. معادلا، گراف دوبخشی گرافی است که دور به طول فرد ندارد.
می توان به U و V به چشم یک رنگ آمیزی مجاز گراف نگاه کرد: اگر همهٔ راس های مجموعهٔ U را آبی و همهٔ راس های مجموعهٔ V را سبز کنیم، دو راس انتهایی هر یال رنگ های متفاوتی خواهند داشت که نشان دهندهٔ یک رنگ آمیزی مجاز برای گراف است. از طرف دیگر، این نوع رنگ آمیزی برای گراف های غیر دوبخشی ( مثل مثلث ) غیرممکن است. مثلاً در مثلث، اگر یک راس را به رنگ آبی و دیگری را به رنگ سبز درآوریم، راس سوم را نمی توانیم با هیچ کدام از این رنگ ها رنگ کنیم، چون این راس به هر دو راس دیگر متصل است.
گراف دو بخشی را معمولاً به صورت G = ( U , V , E ) نشان می دهیم که U و V دو بخش گراف و E مجموعهٔ یال های گراف است. اگر یک گراف دوبخشی همبند نباشد، ممکن است بتوان راس های آن را به شیوه های مختلف به دو بخش تقسیم نمود ( یعنی ممکن است U و V یکتا نباشند ) . در این صورت نمایش G = ( U , V , E ) سودمند واقع می شود؛ چون به کمک آن می توان یک حالت خاص تقسیم رئوس گراف به دو بخش را از بقیهٔ حالات متمایز کرد. اگر | U | = | V | ، گراف G را گراف دوبخشی متوازن می نامیم. اگر درجهٔ تمام راس های U با هم و نیز درجهٔ تمام راس های V با هم برابر باشد، گراف G را گراف دوبخشی شبه منتظم می نامیم.
وقتی رابطهٔ بین دو گروه مختلف از اشیا را مدل سازی می کنیم، معمولاً گراف های دوبخشی به طور طبیعی ظاهر می شوند. به عنوان مثال، فرض کنید یک گراف داشته باشیم که راس های آن نمایانگر بازیکنان فوتبال و باشگاه ها باشند. یک بازیکن را به یک باشگاه وصل می کنیم، اگر آن بازیکن برای آن باشگاه بازی کرده باشد. این گراف نمونه ای از شبکه های وابستگی ( affiliation network ) است. این شبکه ها نوعی گراف دوبخشی هستند و از آن ها در آنالیز شبکهٔ اجتماعی ( social network analysis ) استفاده می شود.
مثال دیگری که در آن، گراف دوبخشی به طور طبیعی ظاهر می شود، مسألهٔ بهینه سازی راه آهن است ( NP - complete ) که در آن، ورودی برنامهٔ حرکت زمانی قطارها و توقف آن ها است و هدف یافتن کوچکترین مجموعهٔ ممکن از ایستگاه های قطار است، طوری که هر قطار در حداقل یکی از این ایستگاه ها توقف کند. این مسئله را می توان به صورت یافتن یک مجموعهٔ غالب در یک گراف دوبخشی مدل سازی کرد که در این گراف برای هر قطار و هر ایستگاه یک راس وجود دارد و یک قطار به یک ایستگاه وصل می شود، اگر آن قطار در آن ایستگاه توقف کند.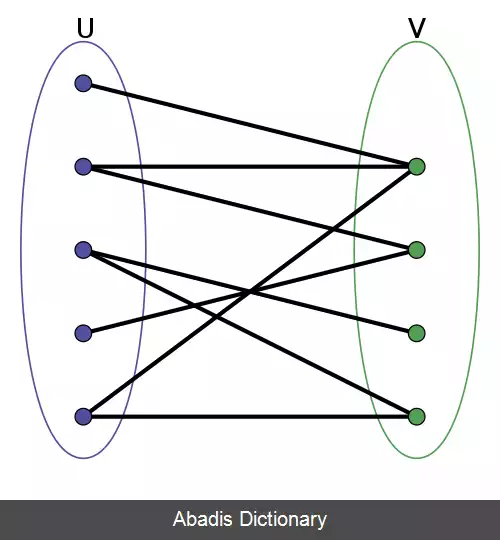
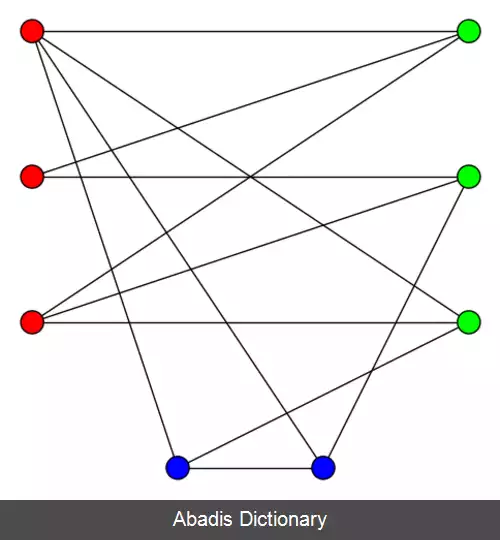
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمی توان به U و V به چشم یک رنگ آمیزی مجاز گراف نگاه کرد: اگر همهٔ راس های مجموعهٔ U را آبی و همهٔ راس های مجموعهٔ V را سبز کنیم، دو راس انتهایی هر یال رنگ های متفاوتی خواهند داشت که نشان دهندهٔ یک رنگ آمیزی مجاز برای گراف است. از طرف دیگر، این نوع رنگ آمیزی برای گراف های غیر دوبخشی ( مثل مثلث ) غیرممکن است. مثلاً در مثلث، اگر یک راس را به رنگ آبی و دیگری را به رنگ سبز درآوریم، راس سوم را نمی توانیم با هیچ کدام از این رنگ ها رنگ کنیم، چون این راس به هر دو راس دیگر متصل است.
گراف دو بخشی را معمولاً به صورت G = ( U , V , E ) نشان می دهیم که U و V دو بخش گراف و E مجموعهٔ یال های گراف است. اگر یک گراف دوبخشی همبند نباشد، ممکن است بتوان راس های آن را به شیوه های مختلف به دو بخش تقسیم نمود ( یعنی ممکن است U و V یکتا نباشند ) . در این صورت نمایش G = ( U , V , E ) سودمند واقع می شود؛ چون به کمک آن می توان یک حالت خاص تقسیم رئوس گراف به دو بخش را از بقیهٔ حالات متمایز کرد. اگر | U | = | V | ، گراف G را گراف دوبخشی متوازن می نامیم. اگر درجهٔ تمام راس های U با هم و نیز درجهٔ تمام راس های V با هم برابر باشد، گراف G را گراف دوبخشی شبه منتظم می نامیم.
وقتی رابطهٔ بین دو گروه مختلف از اشیا را مدل سازی می کنیم، معمولاً گراف های دوبخشی به طور طبیعی ظاهر می شوند. به عنوان مثال، فرض کنید یک گراف داشته باشیم که راس های آن نمایانگر بازیکنان فوتبال و باشگاه ها باشند. یک بازیکن را به یک باشگاه وصل می کنیم، اگر آن بازیکن برای آن باشگاه بازی کرده باشد. این گراف نمونه ای از شبکه های وابستگی ( affiliation network ) است. این شبکه ها نوعی گراف دوبخشی هستند و از آن ها در آنالیز شبکهٔ اجتماعی ( social network analysis ) استفاده می شود.
مثال دیگری که در آن، گراف دوبخشی به طور طبیعی ظاهر می شود، مسألهٔ بهینه سازی راه آهن است ( NP - complete ) که در آن، ورودی برنامهٔ حرکت زمانی قطارها و توقف آن ها است و هدف یافتن کوچکترین مجموعهٔ ممکن از ایستگاه های قطار است، طوری که هر قطار در حداقل یکی از این ایستگاه ها توقف کند. این مسئله را می توان به صورت یافتن یک مجموعهٔ غالب در یک گراف دوبخشی مدل سازی کرد که در این گراف برای هر قطار و هر ایستگاه یک راس وجود دارد و یک قطار به یک ایستگاه وصل می شود، اگر آن قطار در آن ایستگاه توقف کند.


wiki: گراف دوبخشی
پیشنهاد کاربران
پیشنهادی ثبت نشده است. شما اولین نفر باشید
