گراف خود مکمل گرافی است که با مکمل خود یک ریخت است. [ ۱] دوتا از ساده ترین گراف های خود مکمل یک گراف مسیری با ۴ راس و گراف دوری با ۵ راس است.
هر گراف ایده آلی یک گراف خود مکمل است. به طور مثال گراف ایده آل با ۹ راس نام لاتین ۳×3 rook's graph یک گراف خودمکمل است زیرا دارای یک تقارن است که راسی را در مرکز گراف ثابت نگه می دارد و مکان ۴ راس کناری نزدیک مرکز را با ۴ راس گوشه ای شبکه عوض می کند. همهٔ گراف های خودمکمل که به شدت منظم هستند با تعداد راس کمتر از ۳۷ یک گراف ایده آل هستند؛ گراف های ب شدت منظم با تعداد گره ۳۷ و ۴۱ و ۴۹ نیز وجود دارد که[ ۲] نیستند. گراف رادو هم یک گراف خودمکمل نامتناهی است.
هرگراف خود مکمل همبند است. یک گراف خود مکمل با n راس دقیقاً به اندازهٔ نصف تعداد یال های گراف کامل یال دارد به عبارت دیگر 4/ ( n ( n - ۱ و به شرط اینکه تعداد گره بیشتر از ۱ باشد حتماً دارای یک قطر به اندازه ۲ یا ۳ است. چون ( n ( n - 1 باید بر ۴ بخش پذیر باشد پس n به پیمانه ۴ باید با ۰ یا ۱ هم ارز باشد؛ ب طور مثال یک گراف کامل ۶راسه نمی تواند یک گراف خود مکمل باشد.
هر گراف خود مکمل زوج راسی دارای حداقل یک تطابق کامل است.
هر گراف خود مکمل فرد راسی یک راس دارد که با حذف آن گراف باقیمانده همچنان خود مکمل باشد.
مشکل تشخیص همریخت بودن دو گراف و تشخیص خودمکمل بودن یک گراف همان مسئله عمومی همریختی گراف است.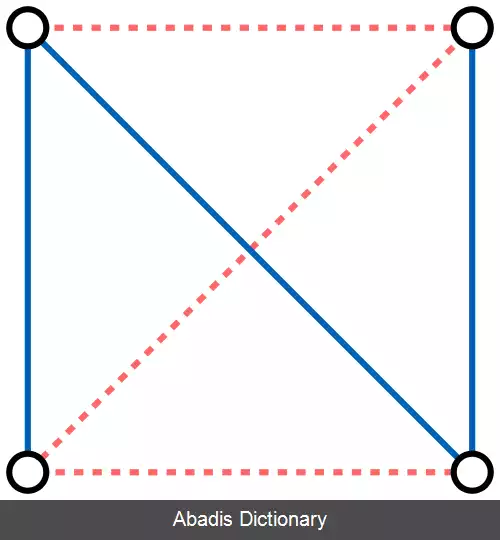
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفهر گراف ایده آلی یک گراف خود مکمل است. به طور مثال گراف ایده آل با ۹ راس نام لاتین ۳×3 rook's graph یک گراف خودمکمل است زیرا دارای یک تقارن است که راسی را در مرکز گراف ثابت نگه می دارد و مکان ۴ راس کناری نزدیک مرکز را با ۴ راس گوشه ای شبکه عوض می کند. همهٔ گراف های خودمکمل که به شدت منظم هستند با تعداد راس کمتر از ۳۷ یک گراف ایده آل هستند؛ گراف های ب شدت منظم با تعداد گره ۳۷ و ۴۱ و ۴۹ نیز وجود دارد که[ ۲] نیستند. گراف رادو هم یک گراف خودمکمل نامتناهی است.
هرگراف خود مکمل همبند است. یک گراف خود مکمل با n راس دقیقاً به اندازهٔ نصف تعداد یال های گراف کامل یال دارد به عبارت دیگر 4/ ( n ( n - ۱ و به شرط اینکه تعداد گره بیشتر از ۱ باشد حتماً دارای یک قطر به اندازه ۲ یا ۳ است. چون ( n ( n - 1 باید بر ۴ بخش پذیر باشد پس n به پیمانه ۴ باید با ۰ یا ۱ هم ارز باشد؛ ب طور مثال یک گراف کامل ۶راسه نمی تواند یک گراف خود مکمل باشد.
هر گراف خود مکمل زوج راسی دارای حداقل یک تطابق کامل است.
هر گراف خود مکمل فرد راسی یک راس دارد که با حذف آن گراف باقیمانده همچنان خود مکمل باشد.
مشکل تشخیص همریخت بودن دو گراف و تشخیص خودمکمل بودن یک گراف همان مسئله عمومی همریختی گراف است.

wiki: گراف خودمکمل
