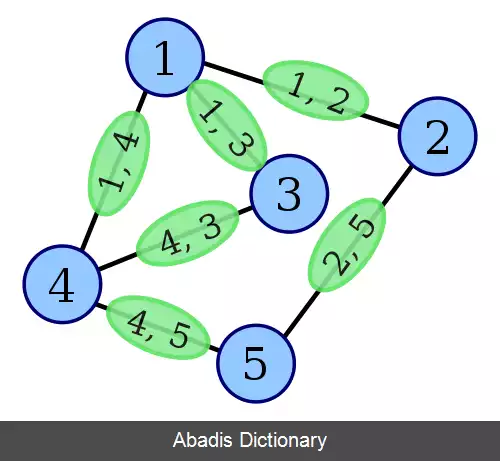
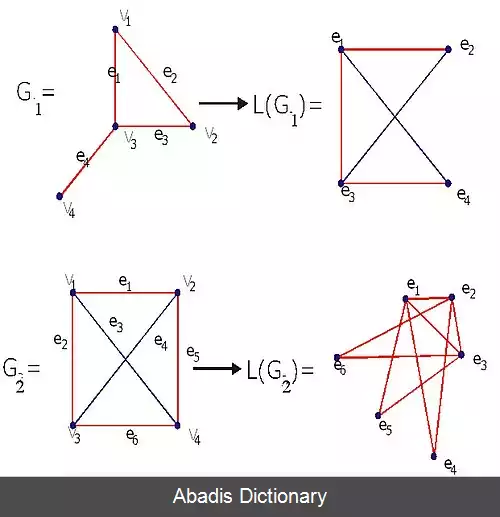
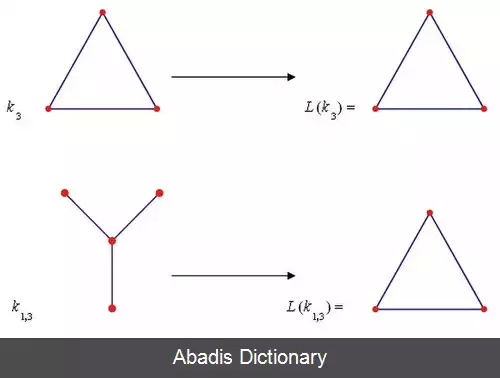
گراف غیر تهی G را در نظر بگیرید. اگر به جای هر یال G راأسی در نظر بگیریم و دو رأس را به هم متصل می کنیم.
در صورتی که یال های متناظر آن دو رأس در G در یک رأس از G با هم مشترک باشند.
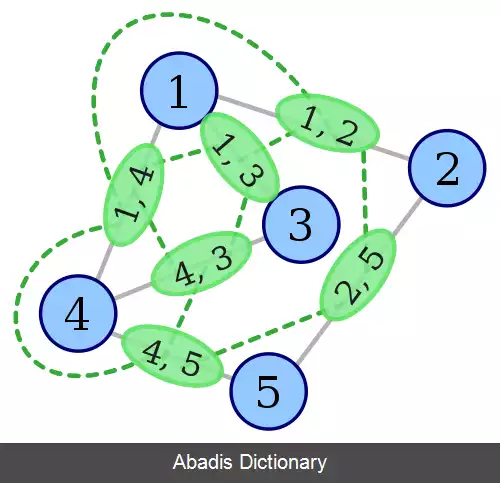
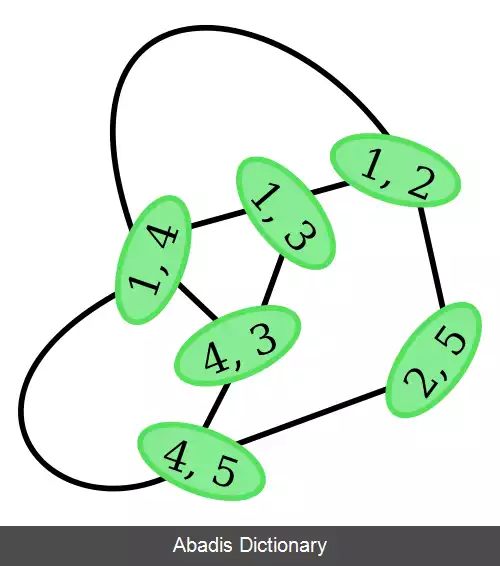
گراف حاصل را با L ( G ) نشان داده و آن را گراف خط می نامیم.
قضیه: اگر G و − r منتظم باشد و دارای n راس، آنگاه L ( G ) نیز منتظم و از درجه 2 ( r − 1 ) می باشد.
اثبات: هر یال گراف G به دو رأس ختم می شود که به هر یک از این رأس ها به جز یال مذکور ، r − 1 یال دیگر وارد می شوند.
یال مذکور تنها با این Z ( r − 1 ) یال رأس مشترک دارد و در این یال رأس گراف L ( g ) است که به Z ( r − 1 ) رأس دیگر متصل است.
پس L ( G ) یک گراف Z r − Z منتظم است.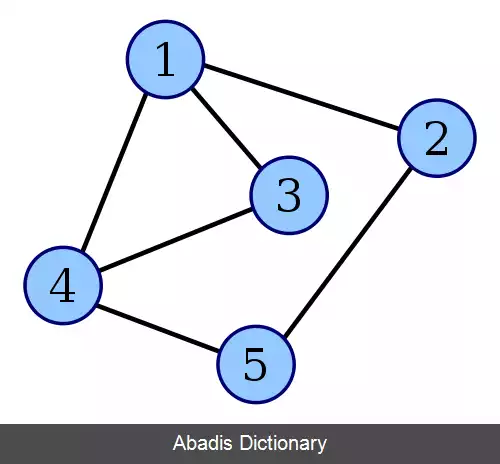
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفدر صورتی که یال های متناظر آن دو رأس در G در یک رأس از G با هم مشترک باشند.
گراف حاصل را با L ( G ) نشان داده و آن را گراف خط می نامیم.
قضیه: اگر G و − r منتظم باشد و دارای n راس، آنگاه L ( G ) نیز منتظم و از درجه 2 ( r − 1 ) می باشد.
اثبات: هر یال گراف G به دو رأس ختم می شود که به هر یک از این رأس ها به جز یال مذکور ، r − 1 یال دیگر وارد می شوند.
یال مذکور تنها با این Z ( r − 1 ) یال رأس مشترک دارد و در این یال رأس گراف L ( g ) است که به Z ( r − 1 ) رأس دیگر متصل است.
پس L ( G ) یک گراف Z r − Z منتظم است.






wiki: گراف خط
