گراف جهت دار و کاربردهای آن. گراف جهت دار D، یک سه تایی مرتب ( ( Ψ ( D و ( A ( D و ( V ( D ) است که تشکیل شده از یک مجموعه ناتهی V ( D ) از راسها و یک مجموعه ( A ( D مجزای از ( V ( Dاز کمانها و یک تابع وقوع ( Ψ ( D که به هر کمان D یک زوج مرتب از راسهای D - که الزاماً متمایز نیستند - را نسبت می دهد. اگر a یک کمان وu, v دو راس باشند به طوری که ( u, v ) = Ψ ( D ) ( a ) ، آنگاه میگوئیم که u, a را به v وصل کرده است؛ u، دم v, a سرa نامیده می شود.
می توانیم به هر گراف جهتدار D، یک گراف G با همان مجموعه راس ها متناظر کنیم، به طوری که به ازای هر کمان از D، یک یال درG با همان دو سر وجود داشته باشد. این گراف، گراف زمینه D نامیده می شود. بالعکس، می توانیم از هر گراف دلخواه G، یک گراف جهت دار بدست آوریم بدین صورت که برای هر یال، یک ترتیب روی راسهای دو سر آن مشخص نماییم. گراف جهت دار حاصل را یک جهت دهی از G می نامیم.
گراف های جهت دار هم، مانند گراف ها، دارای یک نمایش تصویری ساده هستند. یک گراف جهت دار با نموداری از گراف زمینه آن، به علاوه پیکان هایی که سر کمان متناظر با هریال آن را مشخص می کنند، نمایش داده می شود:
هر مفهومی که برای گراف ها برقرار باشد به طور خودکار برای گراف های جهت دار نیز معتبر خواهد بود بنابراین گراف جهت دار شکل ( ۱ ) الف همبند است و هیچ دوری به طول ۳ ندارد، زیرا گراف زمینه آن شکل ( ۱ ) ب، دارای این ویژگی هاست اما مفاهیم بسیاری وجود دارند که شامل مفهوم جهت می باشند تنها برای گراف های جهت دار معتبرند.
یک گشت جهت دار در D عبارتست از یک دنباله متناهی ناتهی ak, uk. . . . . . . , u1 , a1 u0 ) =W ) ، که جمله های آن یک در میان راس و کمان هستند و به ازای i=۱٬۲, …. . , k کمان ai دارای سر ui و دم ui - ۱ است.
همانند گشت ها در گراف ها، غالباً گشت جهت دار ( u0, a1, u1, …. . , ak , uk ) را به طور ساده با دنباله راس های ( u0, u1, …. , uk ) نمایش می دهیم. گذرگاه جهت دار، گشت جهت داری است که گذرگاه باشد. مسیرهای جهت دار، دورهای جهت دار و تورهای جهت دار نیز به طور مشابه تعریف می شوند.
گراف جهت داری که دارای هیچ طوقه ای نیست و بین هر دو راس آن، هیچ دو کمان هم جهتی قرار ندارد یک گراف جهت دار قوی نامیده می شود.
۱ - طراحی یک استوانه کامپیوتری کارآمد
۲ - یک طرفه کردن جاده ها: یک طرفه کردن سیستم جاده ای به طوری که آرایش ترافیک تا حد ممکن حفظ شود.
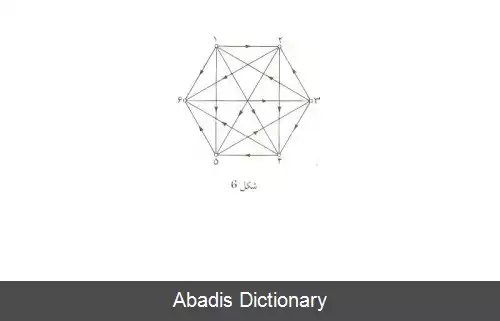
۳ - رتبه بندی شرکت کنندگان در یک تورنمنت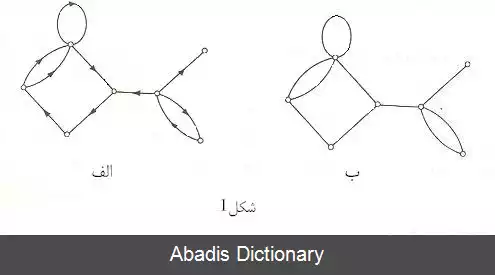
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفمی توانیم به هر گراف جهتدار D، یک گراف G با همان مجموعه راس ها متناظر کنیم، به طوری که به ازای هر کمان از D، یک یال درG با همان دو سر وجود داشته باشد. این گراف، گراف زمینه D نامیده می شود. بالعکس، می توانیم از هر گراف دلخواه G، یک گراف جهت دار بدست آوریم بدین صورت که برای هر یال، یک ترتیب روی راسهای دو سر آن مشخص نماییم. گراف جهت دار حاصل را یک جهت دهی از G می نامیم.
گراف های جهت دار هم، مانند گراف ها، دارای یک نمایش تصویری ساده هستند. یک گراف جهت دار با نموداری از گراف زمینه آن، به علاوه پیکان هایی که سر کمان متناظر با هریال آن را مشخص می کنند، نمایش داده می شود:
هر مفهومی که برای گراف ها برقرار باشد به طور خودکار برای گراف های جهت دار نیز معتبر خواهد بود بنابراین گراف جهت دار شکل ( ۱ ) الف همبند است و هیچ دوری به طول ۳ ندارد، زیرا گراف زمینه آن شکل ( ۱ ) ب، دارای این ویژگی هاست اما مفاهیم بسیاری وجود دارند که شامل مفهوم جهت می باشند تنها برای گراف های جهت دار معتبرند.
یک گشت جهت دار در D عبارتست از یک دنباله متناهی ناتهی ak, uk. . . . . . . , u1 , a1 u0 ) =W ) ، که جمله های آن یک در میان راس و کمان هستند و به ازای i=۱٬۲, …. . , k کمان ai دارای سر ui و دم ui - ۱ است.
همانند گشت ها در گراف ها، غالباً گشت جهت دار ( u0, a1, u1, …. . , ak , uk ) را به طور ساده با دنباله راس های ( u0, u1, …. , uk ) نمایش می دهیم. گذرگاه جهت دار، گشت جهت داری است که گذرگاه باشد. مسیرهای جهت دار، دورهای جهت دار و تورهای جهت دار نیز به طور مشابه تعریف می شوند.
گراف جهت داری که دارای هیچ طوقه ای نیست و بین هر دو راس آن، هیچ دو کمان هم جهتی قرار ندارد یک گراف جهت دار قوی نامیده می شود.
۱ - طراحی یک استوانه کامپیوتری کارآمد
۲ - یک طرفه کردن جاده ها: یک طرفه کردن سیستم جاده ای به طوری که آرایش ترافیک تا حد ممکن حفظ شود.
۳ - رتبه بندی شرکت کنندگان در یک تورنمنت


