در نظریه گراف، گراف تام ( به انگلیسی: Perfect Graph ) ، گرافی است که عدد رنگی آن برای هر زیرگراف القایی اش برابر با مرتبه بزرگترین کلیک آن زیرگراف ( عدد کلیکی ) باشد. به طور معادل می توان تعریف اخیر را برحسب نمادها بیان نماد: گراف دلخواهی چون G = ( V , E ) تام است اگر و تنها اگر برای تمام S ⊆ V داشته باشیم χ ( G ) = ω ( G ) .
گراف های تام شامل خانواده های مهم بسیاری از گراف ها بوده و موجب اتحاد و یکی شدن نتایج رنگ آمیزی ها و کلیک های مرتبط در آن خانواده ها می گردد. به عنوان مثال، در تمام گراف های تام، مسئله رنگ آمیزی گراف، مسئله کلیک ماکسیمم و مسئله مجموعه مستقل ماکسیمم را می توان به صورت زمان - چندجمله ای حل نمود. به علاوه، قضایای متعدد و مهم ترکیبیاتی از نوع مین - مکس، همچون قضیه دیلورث را می توان برحسب تام سازی گراف های خاصی بیان نمود.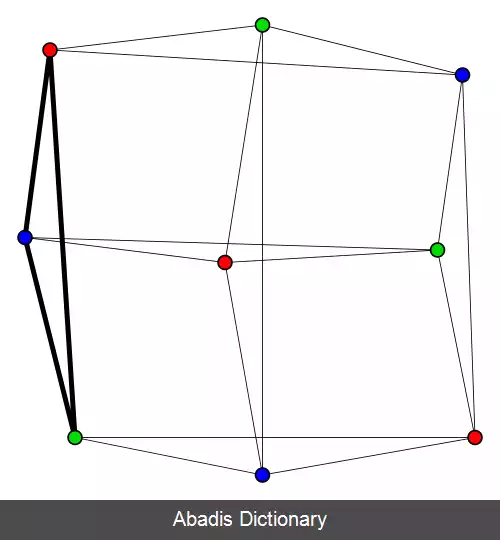
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفگراف های تام شامل خانواده های مهم بسیاری از گراف ها بوده و موجب اتحاد و یکی شدن نتایج رنگ آمیزی ها و کلیک های مرتبط در آن خانواده ها می گردد. به عنوان مثال، در تمام گراف های تام، مسئله رنگ آمیزی گراف، مسئله کلیک ماکسیمم و مسئله مجموعه مستقل ماکسیمم را می توان به صورت زمان - چندجمله ای حل نمود. به علاوه، قضایای متعدد و مهم ترکیبیاتی از نوع مین - مکس، همچون قضیه دیلورث را می توان برحسب تام سازی گراف های خاصی بیان نمود.

wiki: گراف تام
