درمیان گرافهای دو بخشی، k – مکعب ها از اهمیت خاصی برخوردار دارند.
گراف k - مکعب ∗ گرافی است که رئوس آن دنباله های غیر تکراری k تایی از 0 و 1 به صورت ( a1, ak, … , a1 ) باشد. و یالهای آن، میان رئوس رسم شوند که دقیقاً در یک جایگاه متفاوت باشند.
این گراف ها را که با Qk نمایش می دهند خصوصیت های جالبی دارند که پس از چند مثال به خواص آن ها می پردازیم.
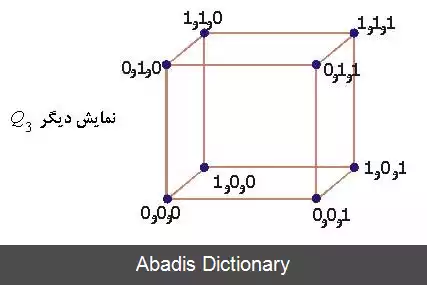
دقت کنید گراف مکعب همان Q3 می باشد که گاهی به صورت زیر نیز رسم می گردد.
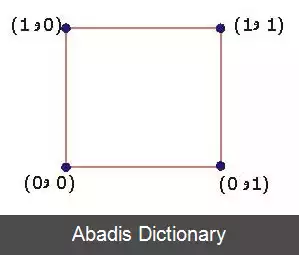
دقت کنید Q3, Q2, Q1 به ترتیب بیانگر فضاهای یک بعدی ( خط ) ، دو بعدی ( صفحه ) و سه بعدی ( فضا ) بوده اند.
ثابت کنید گراف k - مکعب همبند است. کافی است به ازای هر دو راس v, u با دنباله های زیر، مسیری میان آن دو بیابیم.
به طور خلاصه اگر اثبات را بیان کنیم داریم: اگر u با v در m جایگاه تفاوت داشته باشد، از u نخست به راسی می رویم که با u در جایگاه اول از آن m جایگاه متفاوت باشد. سپس از آن به راسی می رویم که علاوه بر جایگاه اول در جایگاه دوم از آن m جایگاه با u متفاوت باشد و به همین ترتیب ادامه می دهیم تا به v برسیم. واضح است چنین مسیری وجود خواهد داشت.
تعداد یالهای گراف k - مکعب را بدست آورید.
برای این منظور نخست تعداد راسها را بدست می آوریم: چون رئوس دنباله های متفاوت k تایی از 0 و 1 می باشند پس بنابر اصل ضرب تعداد آن ها 2k تا می باشد. سپس درجه هر راس را بدست می آوریم: از آنجا که به هر راس یک دنباله k تایی از 0 و 1 متناظر شده و هر راس تنها به رئوسی متصل می گردد که دقیقاً در یک جایگاه با آن تفاوت دارند پس همسایه های هر راس عبارتند از: راسی که فقط درجایگاه اول با آن تفاوت دارد و راسی که فقط در جایگاه دوم با آن تفاوت دارد و. . . تا راسی که فقط در جایگاه k ام با آن تفاوت دارد. و این یعنی درجه هر راس k می باشد پس تعداد یالها = k × 2 k 2 = k 2 k − 1
به راحتی دیده شد گراف k - مکعب، k منتظم می باشد.
ثابت کنید Qk گرافی دو بخشی می باشد.
برای این منظور بایستی رئوس آن را به دو بخش A، B به گونه ای افراز کرد که یالی ما بین رئوس داخل یک بخش موجود نباشد: بدین منظور:
رئوسی که دنباله آن تعداد زوجی عدد 1 دارند = A رئوسی که دنباله آن تعداد فردی عدد 1 دارند = B
حال یالی میان رئوس A وجود نخواهد داشت زیرا اگر وجود داشته باشد. و آن یال uv باشد که v, u ∈ A پس خواهیم داشت: زیرا v, u دقیقاً در یک جایگاه تفاوت دارند ⟶ 1± تعداد 1های u = تعداد 1های v پس v, u نمی توانند از لحاظ زوجیت و فردیت مانند هم باشند. پس یالی که رئوس A را به هم یا رئوس B را به هم وصل کند وجود نداشته و گراف دو بخشی خواهد بود. ( مثال )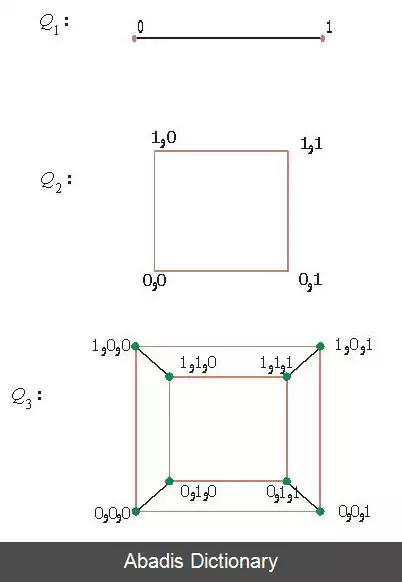



این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفگراف k - مکعب ∗ گرافی است که رئوس آن دنباله های غیر تکراری k تایی از 0 و 1 به صورت ( a1, ak, … , a1 ) باشد. و یالهای آن، میان رئوس رسم شوند که دقیقاً در یک جایگاه متفاوت باشند.
این گراف ها را که با Qk نمایش می دهند خصوصیت های جالبی دارند که پس از چند مثال به خواص آن ها می پردازیم.
دقت کنید گراف مکعب همان Q3 می باشد که گاهی به صورت زیر نیز رسم می گردد.
دقت کنید Q3, Q2, Q1 به ترتیب بیانگر فضاهای یک بعدی ( خط ) ، دو بعدی ( صفحه ) و سه بعدی ( فضا ) بوده اند.
ثابت کنید گراف k - مکعب همبند است. کافی است به ازای هر دو راس v, u با دنباله های زیر، مسیری میان آن دو بیابیم.
به طور خلاصه اگر اثبات را بیان کنیم داریم: اگر u با v در m جایگاه تفاوت داشته باشد، از u نخست به راسی می رویم که با u در جایگاه اول از آن m جایگاه متفاوت باشد. سپس از آن به راسی می رویم که علاوه بر جایگاه اول در جایگاه دوم از آن m جایگاه با u متفاوت باشد و به همین ترتیب ادامه می دهیم تا به v برسیم. واضح است چنین مسیری وجود خواهد داشت.
تعداد یالهای گراف k - مکعب را بدست آورید.
برای این منظور نخست تعداد راسها را بدست می آوریم: چون رئوس دنباله های متفاوت k تایی از 0 و 1 می باشند پس بنابر اصل ضرب تعداد آن ها 2k تا می باشد. سپس درجه هر راس را بدست می آوریم: از آنجا که به هر راس یک دنباله k تایی از 0 و 1 متناظر شده و هر راس تنها به رئوسی متصل می گردد که دقیقاً در یک جایگاه با آن تفاوت دارند پس همسایه های هر راس عبارتند از: راسی که فقط درجایگاه اول با آن تفاوت دارد و راسی که فقط در جایگاه دوم با آن تفاوت دارد و. . . تا راسی که فقط در جایگاه k ام با آن تفاوت دارد. و این یعنی درجه هر راس k می باشد پس تعداد یالها = k × 2 k 2 = k 2 k − 1
به راحتی دیده شد گراف k - مکعب، k منتظم می باشد.
ثابت کنید Qk گرافی دو بخشی می باشد.
برای این منظور بایستی رئوس آن را به دو بخش A، B به گونه ای افراز کرد که یالی ما بین رئوس داخل یک بخش موجود نباشد: بدین منظور:
رئوسی که دنباله آن تعداد زوجی عدد 1 دارند = A رئوسی که دنباله آن تعداد فردی عدد 1 دارند = B
حال یالی میان رئوس A وجود نخواهد داشت زیرا اگر وجود داشته باشد. و آن یال uv باشد که v, u ∈ A پس خواهیم داشت: زیرا v, u دقیقاً در یک جایگاه تفاوت دارند ⟶ 1± تعداد 1های u = تعداد 1های v پس v, u نمی توانند از لحاظ زوجیت و فردیت مانند هم باشند. پس یالی که رئوس A را به هم یا رئوس B را به هم وصل کند وجود نداشته و گراف دو بخشی خواهد بود. ( مثال )






wiki: گراف k مکعب
