کوواریانس یا هم وَردایی[ ۱] ( به انگلیسی: Covariance ) ، در آمار و نظریه احتمالات یک مقیاس برای اندازه گیری «تغییر توأم» دو متغیر تصادفی است. [ ۲] کوواریانس موقعی مثبت است که مقادیر بزرگتر یک متغیر به صورت عمده با مقادیر بزرگتر متغیر دیگر متناظر باشد، و همین تناظر برای مقادیر کوچکتر هم برقرار باشد ( یعنی متغیرها تمایل به رفتار مشابه داشته باشند ) . [ ۳] در حالت مقابل، موقعی که مقادیر بزرگتر یک متغیر به صورت عمده با مقادیر کوچکتر دیگری متناظر باشد ( یعنی متغیرها گرایش به رفتار معکوس داشته باشند ) کوواریانس منفی است. از این رو علامت کوواریانس نشان دهنده نوع گرایش در رابطه خطی بین متغیرها است. تفسیر کردن اندازه کوواریانس ساده نیست زیرا کوواریانس نرمال سازی نشده است، و از این رو بستگی به اندازه متغیرها دارد. نسخه نرمال سازی شده کوواریانس، ضریب همبستگی نام دارد، و اندازه این ضریب قدرت رابطه خطی را نشان می دهد.
باید بین این موارد تمایز قایل شد: ( ۱ ) کوواریانس دو متغیر تصادفی که یک پارامتر جمعیت است و می توان آن را به صورت یک ویژگی از توزیع احتمال توأم دید، ( ۲ ) کوواریانس نمونه که علاوه بر کاربردی که در توصیف کردن نمونه دارد برای مقدار تخمینی پارامتر جمعیت هم از آن استفاده می شود.
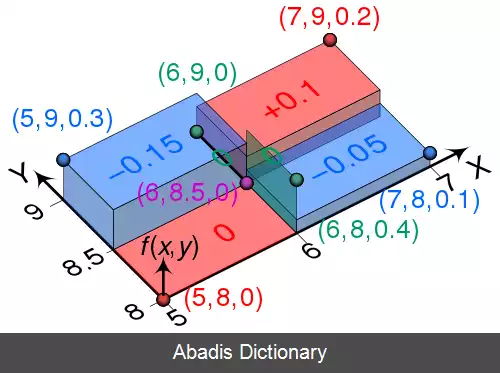
کوواریانس اندازه تغییرات هماهنگ دو متغیر تصادفی است. ( اگر دو متغیر یکی باشند، کوواریانس برابر واریانس خواهد شد ) . برای متغیرهای تصادفی X و Y که امید ریاضی آنها E ( X ) = μ و E ( Y ) = ν هستند، کوواریانس به صورت زیر تعریف می شود:
چنان که دو متغیر تصادفی مستقل باشند، کوواریانس آنها صفر خواهد بود.
فرهنگستان زبان فارسی، وَردیدن از ریشه باستانی وَرت ( وَرتیدن: ریخت باستانی فعل "گردیدن" ) ، را به جای فعل to vary برگزیده است و از آن، مشتقات وردایی ( variance ) ، وردش ( variation ) ، وردا ( variant ) ، هم وردا ( covariant ) ، هم وردایی ( covariannce ) ، ناوردا ( invariant ) ، ناوردایی ( invariance ) ، پادوردا ( contravariance ) را برساخته است.
همپراکنش با همبستگی رابطه دارد؛ چون ضریب همبستگی همان هنجارشده همپراکنش است؛ مثلاً اگر همپراکنش دو تابع صفر باشد، یعنی همبستگی آنها صفر است و این یعنی کلا از هم مستقل هستند. برعکس؛ بالا بودن مقدار همپراکنش چه به صورت منفی و چه به صورت مثبت، مبین آن است که این دو تابع به نوعی به هم وابسته اند. بیشترین مقدار همپراکنش زمانی است که یک تابع خطی بین آن دو تابع قابل تعریف باشد. در این صورت یک متغیر را می توان تابع متغیر دیگر دانست و به جای این که مقادیر آن دو را حفظ کرد، می توان مقادیر یکی به علاوه رابطه آنها را در نظر آورد؛ مثلاً اگر دسته اول جدول یک، درجه حرارت اجاق در ساعات مختلف یک روز بر حسب فارنهایت باشد و دسته دوم اعداد دیگری از این اجاق داشته باشیم و بین این دو دسته یک رابطه خطی به صورت دسته اول منهای سی و دو و کلا ضربدر هجده دهم باشد، خوب! دسته دوم همان دسته اول است منتها بر حسب سیلیسیوس است و نیازی به حفظ آن نیست!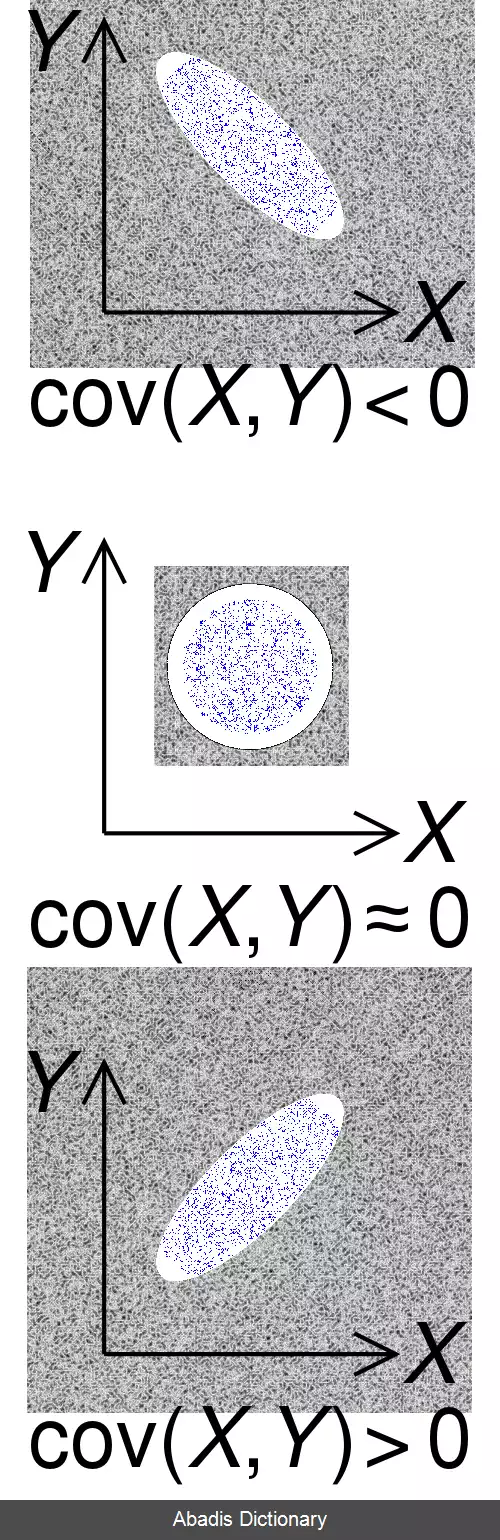
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفباید بین این موارد تمایز قایل شد: ( ۱ ) کوواریانس دو متغیر تصادفی که یک پارامتر جمعیت است و می توان آن را به صورت یک ویژگی از توزیع احتمال توأم دید، ( ۲ ) کوواریانس نمونه که علاوه بر کاربردی که در توصیف کردن نمونه دارد برای مقدار تخمینی پارامتر جمعیت هم از آن استفاده می شود.
کوواریانس اندازه تغییرات هماهنگ دو متغیر تصادفی است. ( اگر دو متغیر یکی باشند، کوواریانس برابر واریانس خواهد شد ) . برای متغیرهای تصادفی X و Y که امید ریاضی آنها E ( X ) = μ و E ( Y ) = ν هستند، کوواریانس به صورت زیر تعریف می شود:
چنان که دو متغیر تصادفی مستقل باشند، کوواریانس آنها صفر خواهد بود.
فرهنگستان زبان فارسی، وَردیدن از ریشه باستانی وَرت ( وَرتیدن: ریخت باستانی فعل "گردیدن" ) ، را به جای فعل to vary برگزیده است و از آن، مشتقات وردایی ( variance ) ، وردش ( variation ) ، وردا ( variant ) ، هم وردا ( covariant ) ، هم وردایی ( covariannce ) ، ناوردا ( invariant ) ، ناوردایی ( invariance ) ، پادوردا ( contravariance ) را برساخته است.
همپراکنش با همبستگی رابطه دارد؛ چون ضریب همبستگی همان هنجارشده همپراکنش است؛ مثلاً اگر همپراکنش دو تابع صفر باشد، یعنی همبستگی آنها صفر است و این یعنی کلا از هم مستقل هستند. برعکس؛ بالا بودن مقدار همپراکنش چه به صورت منفی و چه به صورت مثبت، مبین آن است که این دو تابع به نوعی به هم وابسته اند. بیشترین مقدار همپراکنش زمانی است که یک تابع خطی بین آن دو تابع قابل تعریف باشد. در این صورت یک متغیر را می توان تابع متغیر دیگر دانست و به جای این که مقادیر آن دو را حفظ کرد، می توان مقادیر یکی به علاوه رابطه آنها را در نظر آورد؛ مثلاً اگر دسته اول جدول یک، درجه حرارت اجاق در ساعات مختلف یک روز بر حسب فارنهایت باشد و دسته دوم اعداد دیگری از این اجاق داشته باشیم و بین این دو دسته یک رابطه خطی به صورت دسته اول منهای سی و دو و کلا ضربدر هجده دهم باشد، خوب! دسته دوم همان دسته اول است منتها بر حسب سیلیسیوس است و نیازی به حفظ آن نیست!


wiki: کوواریانس
