در ریاضیات، کنش گروهی ( به انگلیسی: group action ) روی یک فضا، همریختی گروهی از یک گروه به گروه تبدیلات فضا می باشد. به طور مشابه، کنش گروهی روی ساختار ریاضیاتی، همریختی گروهی از یک گروه به گروه خودریختی های آن ساختار است. گفته می شود که گروه روی فضا یا ساختار کنش می دهد. اگر گروهی روی یک ساختار کنش داشته باشد، اغلب روی اشیائی که از آن ساختار ایجاد می گردند نیز کنش می کند. به عنوان مثال، گروه ایزومتری های اقلیدسی روی فضای اقلیدسی و همچنین اشکالی که درون آن ترسیم می شوند نیز کنش انجام می دهد. به خصوص، این گروه بر روی تمام مثلث ها کنش می کند. به طور مشابه، گروه تقارن های یک چندوجهی روی رئوس، اضلاع و وجوه یک چندوجهی کنش انجام می دهد.
کنش گروهی روی فضای برداری متناهی بعدی را نمایش گروهی می نامند. این نوع کنش، امکان می دهد تا بسیاری از گروه ها براساس زیرگروه های G L ( n , K ) شناسایی شوند، یعنی گروه ماتریس های n × n معکوس پذیر روی میدان K.
گروه متقارن S n روی هر مجموعه n عضوی، به وسیله جایگشت عناصرش کنش می کند. گرچه گروه تمام جایگشت های یک مجموعه، به طور صوری به خود مجموعه وابسته است، مفهوم کنش گروهی امکان این را فراهم می آورد تا جایگشت های تمام مجموعه های هم کاردینال، تنها با یک گروه مورد مطالعه قرار گیرند.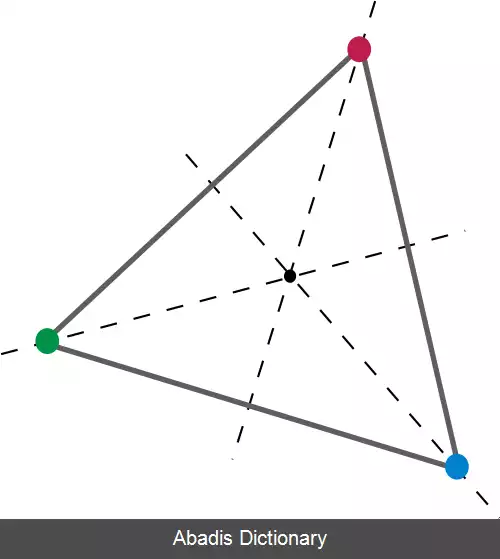
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفکنش گروهی روی فضای برداری متناهی بعدی را نمایش گروهی می نامند. این نوع کنش، امکان می دهد تا بسیاری از گروه ها براساس زیرگروه های G L ( n , K ) شناسایی شوند، یعنی گروه ماتریس های n × n معکوس پذیر روی میدان K.
گروه متقارن S n روی هر مجموعه n عضوی، به وسیله جایگشت عناصرش کنش می کند. گرچه گروه تمام جایگشت های یک مجموعه، به طور صوری به خود مجموعه وابسته است، مفهوم کنش گروهی امکان این را فراهم می آورد تا جایگشت های تمام مجموعه های هم کاردینال، تنها با یک گروه مورد مطالعه قرار گیرند.

wiki: کنش گروهی
