کنترل پذیری شبکه، درمورد کنترل پذیری ساختاری یک شبکه است. کنترل پذیری قابلیت ما برای هدایت یک سامانه پویا، از هر حالت اولیه، به هر حالت پایانی دلخواه، با یک انتخاب مناسب از ورودی ها، در زمان متناهی را شرح می دهد. این تعریف، با تصور مااز کنترل تطابق دارد. کنترل پذیری شبکه های پیچیده ی جهت دار و وزن دار کلی، اخیرا موضوع بحث جدی تعدادی از گروه ها در شبکه های متنوعی در سطح جهانی بوده است. تحقیقات اخیر توسط شارما و همکاران[ ۱] روی شبکه های زیستی چند نوعی، ( شبکه های تعاملی ژن - ژن، ریزآران ای - ژن، پروتئین - پروتئین ) اهداف کنترلی در استئوسارکوما شاخص فنوتیپی را تشخیص داد، که نقش مهم ژن ها و پروتئین های مسئول نگهداری ریز محیط تومور را نشان داد.
داینامیک های زمان - پایدار خطی استاندارد روی شبکه پیچیده X ˙ ( t ) = A ⋅ X ( t ) + B ⋅ u ( t ) را در نظر بگیرید، که در آن بردار X ( t ) = ( x 1 ( t ) , ⋯ , x N ( t ) ) T حالت یک سیستم از N راس در زمان t را اختیار می کند. ماتریس N × N ، A ، نمودار سیم کشی سیستم و قدرت برهم کنش بین اجزا را توصیف می کند. ماتریس N × M ، B ، راس های کنترل شده توسط یک کنترل کننده ی خارجی را مشخص می کند. سیستم توسط بردار ورودی وابسته به زمان u ( t ) = ( u 1 ( t ) , ⋯ , u M ( t ) ) T ، که کنترل کننده بر سیستم تحمیل می کند، کنترل می شود. برای تشخیص کمینه تعداد رئوس راهبر که با نماد N D نمایش داده می شود، که کنترل آن برای کنترل کامل دینامیک های سیستم کافی است، لیو و همکاران[ ۲] تلاش کردند که ابزارهای نظریه کنترل ساختاری را با نظریه گراف و فیزیک آماری ترکیب کنند. آنها[ ۲] نشان دادند که کمینه تعداد ورودی یا رئوس راهبر مورد نیاز برای اعمال کنترل کامل بر روی شبکه، با بیشینه تعداد تطابق در شبکه تعیین می شود، که همان بیشینه مجموعه ای از یال هاست که راس ابتدا و انتها مشترک ندارند. از این نتیجه یک قالب تحلیلی بر پایه توزیع درجه ورود خروج ایجاد شد تا n D = N D / N را برای گراف های مقیاس آزاد و اردوش - رنیی پیش بینی کند. [ ۲] هرچند اخیرا نشان داده شده که کنترل پذیری شبکه ( دیگر روشهای تنها - ساختار که فقط همبندی گراف را استفاده می کنند، A ، برای ساده سازی دینامیک های اصولی ) ، از تعداد و انتخاب مجموعه های راس های راهبر که به بهترین وجه دینامیک های شبکه را کنترل می کنند، هم فرو جهش می کند هم اضافه جهش، که اهمیت افزونگی ( مانند کانالیزه کردن ) و دینامیک های غیرخطی در تعیین کنترل را برجسته می کند. [ ۳]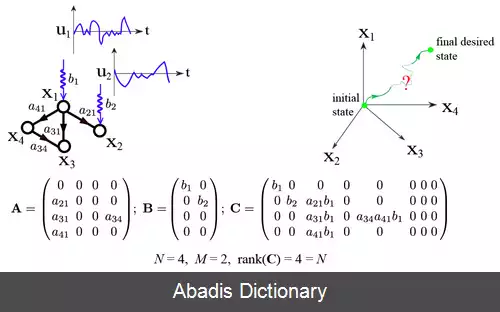
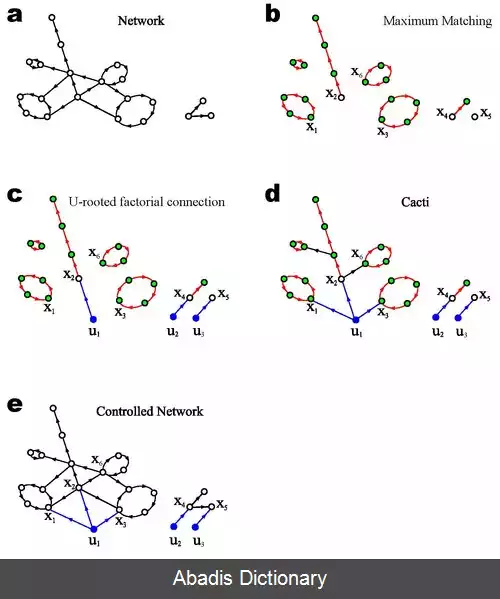
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفداینامیک های زمان - پایدار خطی استاندارد روی شبکه پیچیده X ˙ ( t ) = A ⋅ X ( t ) + B ⋅ u ( t ) را در نظر بگیرید، که در آن بردار X ( t ) = ( x 1 ( t ) , ⋯ , x N ( t ) ) T حالت یک سیستم از N راس در زمان t را اختیار می کند. ماتریس N × N ، A ، نمودار سیم کشی سیستم و قدرت برهم کنش بین اجزا را توصیف می کند. ماتریس N × M ، B ، راس های کنترل شده توسط یک کنترل کننده ی خارجی را مشخص می کند. سیستم توسط بردار ورودی وابسته به زمان u ( t ) = ( u 1 ( t ) , ⋯ , u M ( t ) ) T ، که کنترل کننده بر سیستم تحمیل می کند، کنترل می شود. برای تشخیص کمینه تعداد رئوس راهبر که با نماد N D نمایش داده می شود، که کنترل آن برای کنترل کامل دینامیک های سیستم کافی است، لیو و همکاران[ ۲] تلاش کردند که ابزارهای نظریه کنترل ساختاری را با نظریه گراف و فیزیک آماری ترکیب کنند. آنها[ ۲] نشان دادند که کمینه تعداد ورودی یا رئوس راهبر مورد نیاز برای اعمال کنترل کامل بر روی شبکه، با بیشینه تعداد تطابق در شبکه تعیین می شود، که همان بیشینه مجموعه ای از یال هاست که راس ابتدا و انتها مشترک ندارند. از این نتیجه یک قالب تحلیلی بر پایه توزیع درجه ورود خروج ایجاد شد تا n D = N D / N را برای گراف های مقیاس آزاد و اردوش - رنیی پیش بینی کند. [ ۲] هرچند اخیرا نشان داده شده که کنترل پذیری شبکه ( دیگر روشهای تنها - ساختار که فقط همبندی گراف را استفاده می کنند، A ، برای ساده سازی دینامیک های اصولی ) ، از تعداد و انتخاب مجموعه های راس های راهبر که به بهترین وجه دینامیک های شبکه را کنترل می کنند، هم فرو جهش می کند هم اضافه جهش، که اهمیت افزونگی ( مانند کانالیزه کردن ) و دینامیک های غیرخطی در تعیین کنترل را برجسته می کند. [ ۳]


wiki: کنترل پذیری شبکه
